14: London Tsai - The Reclusive Dean of The New Escherians
| The Reclusive Dean of The New Escherians | |

| |
| Information | |
|---|---|
| Guest | London Tsai |
| Length | 01:02:55 |
| Release Date | 30 November 2019 |
| YouTube Date | 25 January 2020 |
| Apple Podcasts | Listen |
| Links | |
| YouTube | Watch |
| Portal Blog | Read |
| All Episodes | |
What happened to the Mathematical and Scientific art movement after MC Escher? It went underground.
In this episode of the Portal, Eric begins tracking down the leaders of this hidden movement; one that is smuggling higher level science into transcendent art forms. Eric had to coax one the movement’s foremost members, London Tsai, to come out of obscurity where he had been preserving his mathematical art in sarcophagi of unopened bubble wrap sitting for decades in various New York City studios.
London is just the first of these New Escherians we’ll be profiling. These modern day Prometheans are stealing higher level mathematics from the professorial priesthood replacing the Seraphim and Cherubs of antiquity with topological paintings, protein sculptures, and light symphonies that speak to our hearts, minds and desires for transcendence. The podcast will be released later with video showing a taste of Tsai's groundbreaking work.
Sponsors[edit]
Lamps Plus: Get up to 50% OFF hundreds of lights, furniture and décor between November 25 and December 24 go to LampsPlus
Wine Access: Get $100 off your first purchase of $250 or more visit WineAccess
Skillshare: Two whole months of unlimited access to thousands of classes for free visit SkillShare
Transcript[edit]
Episode 14 VTT File (raw file)
The Portal Group's Transcript Completion Project generates and edits transcripts for content related to Eric Weinstein and The Portal Podcast. Completed transcripts are available to read on The Portal Blog and The Portal Wiki. If you would like to contribute, you can make direct edits to the wiki, or you can contact Aardvark or Brooke on The Portal Group Discord Server.
This transcript was generated with Otter.ai by Brooke from this content's YouTube version. It was edited by Aardvark#5610. Further corrections and contributions were provided by Tim (TimMelon#7940).
Housekeeping[edit]
00:00:00
Eric Weinstein: Hello everyone. The episode you're about to see has held up our YouTube channel for a while. It was recorded remotely in New York City along with two other episodes, and apparently it is a bit blurry. We couldn't control for it. We tried correcting it digitally, but that met with only limited success. There was a question about whether to release a still image over this audio, but we decided instead to release the blurred product because, in fact, it is a visual episode with artist London Tsai. We hope we've made the right decision. We apologize for the blurriness and the fact that it has held up the sequence of releases. But given that we've now decided to bite the bullet, we hope to return to releasing episodes on a regular basis on this channel. We hope you like it. We think very highly of London Tsai and we hope to have him back on the program, hopefully with a little bit better focus.
Introduction[edit]
00:00:59
Eric Weinstein: Hello, you've found The Portal. I'm your host, Eric Weinstein, and I'm here in Manhattan with artist London Tsai, a person I've been looking to meet for quite some time, and I just met him yesterday for the first time. London, welcome.
00:01:13
London Tsai: Thank you.
00:01:14
Eric Weinstein: So, I have been eyeing your artwork for years on the internet. I've used it in talks. And you're one of the most important people that we've had come on The Portal, even though very few people will know who you are or what you've been up to. Can you say a little bit about your background as a mathematical artist?
00:01:40
London Tsai: Oh my background. So my background as an artist... Well, I studied mathematics in undergrad, and—maybe I should start over. So actually, I went to college.
00:01:56
Eric Weinstein: So you admit you went to college.
00:01:58
London Tsai: Yeah I did, and I wanted to actually study French literature and international relations. And my freshman year, I took the standard courses, and I really delved into 20th century French literature.
00:02:20
Eric Weinstein: This was at Duke?
00:02:21
London Tsai: This was at Tufts.
00:02:22
Eric Weinstein: Oh at Tufts. Okay.
00:02:23
London Tsai: So at Tufts, I took all these liberal arts classes, humanities classes, and I was actually disappointed. I had all these ideas about what I wanted to accomplish in literature and what I would learn, and I would ultimately find some sort of meaning, you know, some understanding of the world we live in. And instead I was frustrated, and I didn't seem to be able to get answers to the questions I had. And to my surprise, I was enjoying calculus much more than any of the classes I took.
00:03:04
Eric Weinstein: Dear sweet child.
00:03:04
London Tsai: Yeah, I know. So what happened was that in my sophomore year, I declared my math major.
00:03:13
Eric Weinstein: Okay, so you came out of the closet.
00:03:15
London Tsai: Came out closet, yeah.
00:03:18
Eric Weinstein: Outed yourself as a proto-mathematician—
00:03:21
London Tsai: Yes.
00:03:22
Eric Weinstein: And... then?
00:03:25
London Tsai: And then I—well, I grew up in a artistic household, and I always thought I would do some sort of artwork. But once I discovered mathematics, I found that it is more artistic than anything that I had ever seen before: is more creative, is more ingenious, is more abstract.
00:03:59
Eric Weinstein: With no author, no—
00:04:01
London Tsai: No author, yeah. And it's just, it's just there, and you could study it, and it was infinitely deep. You could pick up any part and you could just keep going, and everything just fit together so nicely, and I just wanted to see more and understand more. And, you know, all the mathematical writing that was on the blackboards, like from the graduate classes and things like that, I wanted to understand what they were about—and they must be representatives of some sort of world that I didn't have access to at the time.
00:04:47
Eric Weinstein: So I'm looking into your eyes and I'm seeing something that looks like a religious convert, or maybe like Ray Charles the first time he tried heroin, or something. But you got the bug.
00:04:56
London Tsai: Absolutely.
00:04:57
Eric Weinstein: Okay.
00:04:57
London Tsai: Yeah, absolutely. I mean, it was the only thing I thought about for about six years. I just...
00:05:04
Eric Weinstein: You're obsessed.
00:05:05
London Tsai: I just dived into it. In fact, I don't think I had this really strong mathematical ability, I was just fascinated by it. And for me, it didn't come as naturally as it did for my brother, and I really had to struggle. I really had to—I felt it was a real challenge to my self-worth. I felt like if I couldn't do this, if I couldn't understand mathematics, that life was just not worth living.
00:05:44
Eric Weinstein: Woah.
00:05:45
London Tsai: It was pretty—it was like that. I just decided I would prove to myself that I could do it, and to the exclusion of almost everything else.
00:05:54
Eric Weinstein: Well this is, I mean, I'm joking around a little bit about heroin, but it does behave like that. Once you find out that there is a hidden world, and that this hidden world is strangely meaningful, and that it's clearly too beautiful to be constructed by any human mind... Like the most beautiful human minds can barely understand this world, but it's more like they're dusting off—I guess in my understanding, I think about the ruins of Petra, and imagine that Petra were buried in sand and you were just whisking away sand and uncovering ruins. You'd be pretty convinced that you weren't authoring the ruins of Petra. You would know that you didn't build this thing. But you, you know, it's just such a privilege to be able to touch something this beautiful that is apparently unauthored by anything known to be human.
00:06:45
London Tsai: I mean, that's kind of my feeling of—
00:06:47
Eric Weinstein: So like, of reverence and transcendence.
00:06:50
London Tsai: Yeah, like there's this kind of eternal stillness in this world, you know. Recently I've just picked up my old math texts, and the ideas there are just as fresh as they were, you know, 30 years ago when I was studying them, and they still have that pure beauty about them.
Sheet Music for Mathematics[edit]
00:07:18
Eric Weinstein: Well, let me let you in a little bit on why I'm having you on this program. It's not just because I'm so devoted to your work, it's also because my belief is that we have the most beautiful symphonies in the world locked inside of our journals, and our math libraries, let's say, as text. And, you know, you can ask, "Well, if you have a symphony of Brahms, is it a symphony if it only resides in the sheet music and is never performed?" Now that's a very disturbing question, because the instructions for its performance are present. And it may be that a tiny number of people can actually read a sheet of sheet music and say, "Oh my God, that's gorgeous," because they can hear it in their head. But the rest of us actually need the thing to be performed. And yet, there is no orchestra—or analog of an orchestra—that performs works of great mathematical or physical beauty.
00:08:22
London Tsai: Yeah. That's true. I mean, part of my interest in mathematics initially was that I could take mathematics and the beautiful images that I saw in my mind during math class, and bring them out as artistic things.
00:08:42
Eric Weinstein: Well, so this is where I start to also get a little bit pissed off with you, which is—
00:08:46
London Tsai: [Laughter]
00:08:47
Eric Weinstein: No, I'm not kidding. I'm angry about the fact that we have these papers and books that form the sheet music that's never performed. And then I find out that you exist, and that you have been performing and recording—effectively—these masterworks, and then what do you do with the vinyl? You put it under bubble wrap in some loft in Soho, in Manhattan, and it doesn't come out for years or decades at a time. So effectively, you're sitting on some of the only known recordings, if you will, of some of the great masterworks of the mathematical universe. WTF, London? What are you doing, man?
00:09:35
London Tsai: Well, I think what's happened is that I'm always kind of interested in the next idea, or the next theorem, or the next project, and all these things that are made by me just sort of... You know, after I'm done with, it's not—it doesn't seem that important anymore.
Fiber Bundles & Visualizations[edit]
00:10:05
Eric Weinstein: Well, I think that's great for the artist, but whoever's doing your PR and marketing, I'm firing them and taking over. So, here's the thing that I get. As somebody who studied mathematics, I had the same feeling. I wasn't necessarily made to do mathematics, that wasn't how my brain—it didn't find the symbolic layer very easy. But I was exposed to things of such beauty and depth that I couldn't find any other analog on planet Earth. Once you understand how rich the mathematical universe actually is, you can't believe that it was somehow just created out of logical necessity.
00:10:47
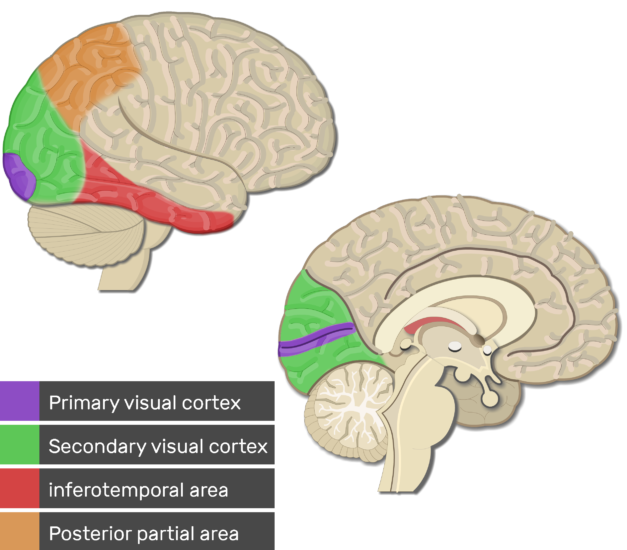
And there's a tiny portion of it that is actually visualizable by our visual cortex. And, what's odd is that when we talk about things as being visual in mathematics, we're often talking about things that we can't actually see. We have an intuition that comes from 1, 2, and 3 dimensions, and then we have to take that intuition—where we can actually visualize something, we construct a model of it—and we have a series of tricks by which we use our minds to visualize things that we can't actually see. I mean, I don't even know what to call this process. I'm not sure if it has a description.
00:11:31
London Tsai: Yeah, I know what you mean. It's definitely an intuition that you have, and it's some kind of vague mental image. And I, what I have to do is I have to somehow, in my artwork, I have to take this vague mental image and try to make it concrete. And it's, it's not always—
00:11:57
Eric Weinstein: Well, this is the thing. Now keep in mind that there are gonna be people who are listening to this as audio, and then we will later release it as video—and I don't know how much of it will be seeable on the channel. But one of the things that is very interesting to me is that what happens in our minds, when we really start to open the portal to the deepest secrets that the universe has to offer, is that we use this mixture. And the mixture is some amount of the world that we can construct as models, so that we can actually directly visualize it, as if we could use our eyes to make a clay model of, let's say, an algebraic variety or what have you. And then there's this extra intuition that we have to build in from texts and from symbology to remind ourselves that usually we're not able to see the full totality of whatever it is we're discussing.
00:12:45
And your art very often has a geometric picture together with prose that is kind of fading in and out of perceptibility, together with a bunch of mathematical symbols that are describing what has been constructed. And I thought that what's very interesting is that that actually mirrors what a mathematician's model is of one of these higher structures that can't be seen directly. But it's basically intuition from a low-dimensional thing that can be visualized, together with prose and mathematical symbols that actually rigorously describe the object. And so that—in some sense—it is a faithful recreation by combining gorgeous form together with text, and prose, and symbology, in order to recreate the mathematical state that we mean by saying that mathematics is very visual.
00:13:47
So for example, behind you right now, there's an amazing painting that I've seen for years—and I think I've actually used it in a talk at Columbia as the cover art for the first slide—of what I assume is Heinz Hopf's famous fibration from the early 1930s. And so it's the series of interlocking partial torii, each of which is filled up by circles, and it's a very impressionistic, but also somewhat rigorous, description of this object that on the Joe Rogan program I said may be the most important object in the universe, because when we talk about physics being ultimately a theory of waves, we want to know, well, what are those waves waves in? What is the analog of the ocean for an ocean wave inside of physics?
00:14:53
So, those waves are waves in bundles, and the bundles come in two basic types for most purposes. One is called a principal bundle, which is what you have behind you. And you've been so good as to put a depiction of another kind of bundle, which is sort of even closer to the wave concept, a vector bundle, which is what is behind me. Now I think it's very strange that we have all of these programs, let's say on public television, or Brian Green talking about the elegant universe, and all of these things, and yet when I ask people, "Well, do you know—You're interested in wave-particle duality, do you know what the waves are waves in?" Nobody seems to know about bundles.
00:15:35
London Tsai: It's surprising.
00:15:36
Eric Weinstein: Well, it's disturbing, and the idea is that there are very few people depicting bundles artistically. And essentially, the only person doing it is hiding their artwork away so that nobody even knows it's there.
00:15:56
J'accuse—well, no, I mean, this is an important link. I guess this is what I'm trying to say, is that you are somehow breaking the secrecy. It's like, you know, Prometheus gave fire to man. Okay, well you are now bringing bundles to the masses. And I think it's fantastic because it allows people to skip the symbolic step, which is usually what leaves them out of participating—at least as observers—of the amazing museum of mathematical finds. Can you talk a little bit about what caused you to do these two works? The principal bundle behind you, which—what do we call this Hopf fibration behind you?
00:16:46
London Tsai: Yeah, call it The Hopf Fibration.
00:16:47
Eric Weinstein: And behind me?
00:16:49
London Tsai: Call it Purple Vector Bundle.
00:16:51
Eric Weinstein: Purple Vector Bundle. All right, so we've got a principal bundle, which is The Hopf Fibration, [and] a Purple Vector Bundle. Talk to me about what you were thinking when you created them.
00:17:00
London Tsai: So I had the fortune in undergrad to be the first advisee of an algebraic geometer. She was an assistant professor at the time. Her name is Montserrat Teixidor, and she's actually quite known in algebraic geometry. And she had this kind of deep, quiet confidence about her. And I would go to her office hours religiously, and I would sit there and annoy her with my questions from undergrad math. But she was always working with a little pencil, sharpened all the way to the eraser almost. And she would be always writing the word—that "Let f be a fiber bundle."
00:17:46
And so I was a freshman and I was thinking to myself, 'What the heck is a fiber bundle?' No one's ever told me about that. And so one of the goals in studying math was to figure out just what it was that she was thinking about, what were these fiber bundles that she was constantly writing about. And so, in my mind, I always had this idea that I needed to understand that. And so that was kind of probably the germ of my interest in bundles.
00:18:19
And then later on in grad school, I encountered them. And then later on, when I started painting, I just—I don't know, we were talking about intuition earlier, and I just feel like there's some sort of seeds in us when we see lots of mathematical things, or anything in the world for that matter. There's something that tells us there's some content here, and that this is worthy of our attention. And somehow these bundles—vector bundles, fiber bundles, principal fiber bundles—were just objects that to me were worthy of sinking a lot of time, and thought, and making artwork of. So I don't really know what it was that drew me to them, except that I was drawn to them.
00:19:10
Eric Weinstein: Have you ever read C.N. Yang, of Yang–Mills theory fame, talking about his discovery of the importance of fiber bundles?
00:19:19
London Tsai: I think I have, yeah. It's a short essay, right?
00:19:22
Eric Weinstein: He's written a few, I think. But he talks about—and I wish I had the exact quote here—Einstein was questing for a structure to unify physics. And in Yang's estimation, the fiber bundle was the answer to Einstein's quest. Now of course, this cropped up in something called Kaluza–Klein theory. Einstein used what we would now call the tangent bundle and cotangent bundle of spacetime. So he would—let's just throw some jargon out there. So a fiber bundle is sort of like the xy-plane growing up and going off to graduate school, and the analog of the x-axis would be called the base space, and the y-axis and all its translates—those vertical lines—would be called the fibers, and the xy-plane would be called the total space.
00:20:19
And in that story, the x-axis gets replaced by spacetime, and the y-axis gets replaced by various things, like a 16-dimensional vector bundle to give the particles their 16 dimensions-worth of personalities. There are these things called spinors that are attached to something that you can visualize as the Philippine wineglass dance. Sometimes you call this the principal bundle that governs all of particle theory the SU(3) x SU(2) x U(1) bundle over spacetime. And where each of those weird—SU(3), for example—is what we'd call a collection of symmetries that form what mathematicians term a group. Same thing with SU(2). And U(1) is just a fancy name for the circle.
00:21:21
So behind you, what you see is a simplified version of a principal bundle that we might use for doing physics research. But this one lives on top of a 2-dimensional sphere, like the surface of the earth, and it adds an extra circle for every point in space and time. And those are the lines—as I understand it—that are in these partial torii that are nested behind you. So you're—it's pretty tough going—but you're almost able to visualize the structure on which electromagnetism—which is how you and I are looking at each other through photon exchange, and the way in which, like if these microphones have magnetic membranes that are turning our pressure waves into electrical impulses—all of that is described in some sense by patterns attached to the circles on that painting, upgraded to make it a story of space and time rather than just a story of circles over a 2-dimensional surface of the globe. So it'd be pretty crazy if it wasn't like one of the coolest looking objects in the universe.
00:22:52
London Tsai: It is pretty cool. I mean, the interesting thing about painting it, or making it visual, is that you actually have to cut away parts to reveal what's the actual structure
00:23:02
Eric Weinstein: Because it's too densely packed.
00:23:03
London Tsai: It's too densely packed. So I'm only picking a select few of these torii. I am only showing parts of them so I can actually reveal what's underneath, because they're all nested.
00:23:19
Eric Weinstein: Now the odd thing is that before I knew about your work, I think, and before I knew about—I don't know if you've encountered Dror Bar-Natan, who came up with a picture of this, which he termed Planet Hopf, which I used—
00:23:30
London Tsai: Yeah, yeah, yeah, I think you pointed me to it.
00:23:32
Eric Weinstein: Now I did version of this in a Python release by a group called Enthought, and I got them to help me out. I had to use the transparency of some of the visual structures to allow me to see through so I didn't have the occlusion phenomenon. You don't have that luxury with paint. It is very tough to see, but the fact that it can be seen—and I think this is the really interesting thing—means that a giant chunk of physics and mathematics is almost within reach of the person who can't trust her or his ability to negotiate the world of mathematical symbols.
00:24:17
And, you know, this is a huge problem—that a lot of people think that they're bad at music in the West because our music is so dependent on notation. However, in lots of cultures, notation isn't what carries music, it's just personal instruction. And a lot of those people who are bad at symbols would be good at music if it were in any other culture that wasn't symbolically so dependent. And I view this as being, well, what if I was in a culture in which mathematics wasn't transmitted as much symbolically? Fair, unfair?
00:24:52
London Tsai: It's an interesting approach. I'm not wholly sure, but yeah, I can, maybe I can buy that. Because one of the things that drew me to math was the actual, the actually, the symbols, actually—
The Mathematical Art Movement[edit]
00:25:05
Eric Weinstein: Well, I want to talk about this mathematical art movement that has never been named.
00:25:11
London Tsai: Okay.
00:25:12
Eric Weinstein: I'm going to try to figure out what name to give it later. But, tell me if any of the following have impacted you. John Archibald Wheeler, who was Feynman's teacher. Very famous physicist. He seemed to have an incredible passion for doing the kinds of things you're doing on blackboards to give these masterful lectures. Have you ever encountered his blackboard?
00:25:41
London Tsai: No, I haven't.
00:25:41
Eric Weinstein: Okay. Let me try another one. Roger Penrose, who wrote The Road to Reality, is of course a relatively famous person, drew the first copy of the Hopf fibration that I had ever seen. It is strikingly like your own. Have you seen that?
00:25:58
London Tsai: I have. I have that book, The Road to Reality. And I have some some of his more recent books as well. But I think the first picture of a Hopf fibration I ever saw was Bill Thurston's, in his Three-dimensional Geometry and Topology.
00:26:14
Eric Weinstein: Oh, were these the Princeton lecture notes that were never released as a book, or do they eventually become a book?
00:26:20
London Tsai: It eventually became book.
00:26:21
Eric Weinstein: Okay, yeah, this is the thing, is that mathematicians would trade these these mimeograph notes that weren't quite books, but we would all look at them and we felt like we were looking into secret tomes that only some people could have.
00:26:35
London Tsai: That's right. I think later it became a book, and that's when I when I first saw it.
00:26:38
Eric Weinstein: So Bill Thurston, of course, was famous within mathematics as being a Fields medalist, who contributed to Grisha Perelman's program for solving the Poincare conjecture in dimension 3, proving that any sphere that was sufficiently simple from its algebraic properties had to actually be the 3-dimensional version of the sphere.
00:27:03
Did you know Bill Thurston at all?
00:27:05
London Tsai: I didn't. I knew people who knew him.
00:27:10
Eric Weinstein: I knew him a little bit. He came through Harvard when I was a graduate student there. And one of one of the comments he made, he said, "You want to know what keeps this field great?" And I said, "Tell me." He said, "In any other field, if a Fields medalist came through, that's like a Nobel Prize winner at the top of the field. It would be a big deal." And he said, "Here I am sitting with a bunch of you guys at some salad bar after my talk, because we're just not that pretentious." And I thought, 'That's interesting,' because he recognized that he would be a big shot and he really valued the fact that nothing was being made over his presence beyond the mathematics.
00:27:50
London Tsai: That's a great, yeah. In fact, I was reading his book on my honeymoon. I brought it along—
00:28:00
Eric Weinstein: Oh you really have it bad, sir.
00:28:04
London Tsai: We were in Honolulu and we had this nice place with a beautiful lanai, and here I was reading Thurston. And that's when I saw—
00:28:15
Eric Weinstein: Well, you had to be surrounded by beauty, of course.
00:28:18
London Tsai: Yes, I was.
00:28:23
Eric Weinstein: What is it that you think you're supposed to be doing? I mean, you have this ability to understand mathematics, and you have the ability to look into your own mind and see, well, how is it registering? And then you have the ability to externalize it. That's a relatively unusual skillset. I mean, there's—I should continue mentioning the remaining names, like Fomenko is this crazy mathematical artist. I like the fact that Bathsheba Grossman is doing some beautiful mathematical sculpture. A guy named Nico Meyer, in—I guess—Temecula, is doing Hopf fibration sculpture right now.
00:29:05
London Tsai: Really? Wow, okay.
00:29:07
Eric Weinstein: Well in part because, you know, we're now talking about this on these large programs, and rather than people just turning off and saying, "Well, I don't know what that was," because it's visual people are getting super intrigued and just going out and trying to learn the math for themselves, including artists. So I think that what there needs to be is a movement. I mentioned an artist named Luke Jerram, who did these beautiful glass sculptures of pathogens and viruses, and he does malaria and HIV and it's just absolutely, stunningly beautiful. Who are—obviously M.C. Escher is probably the biggest mathematical artist of them all. Why aren't there more people working in this movement? Why isn't the movement named? Why aren't you guys collected? Why aren't there exhibitions of this stuff? Why why why why why?
00:30:07
London Tsai: I don't really know. It could be that the people who feel that they can actually do this stuff don't really have... Maybe it's just that mathematics is too attractive to them, you know? It's like you'd rather do math than make paintings about math, or make representations of it, you know? It's so much more beautiful to spend your time—like, the analogy I have is of a mountaineer. You'd rather be out climbing your mountains than—
00:30:47
Eric Weinstein: Yeah, but, all right. I'm gonna take issue with you here.
00:30:48
London Tsai: Okay.
00:30:51
Eric Weinstein: Tell me you don't feel cut off from people who you can't show this to. Like you've gone some place on a trek as a mountaineer, which is so spectacularly gorgeous you can't even believe that it exists, and you have somebody you love who's not knowledgeable. And you're trying to figure out well, can I charter a helicopter? Can I get this person to get into really good physical shape and make the long trek? Is there any way I can bring back a picture that can communicate—I guess I feel cut off from everyone on the planet who hasn't seen that this stuff exists and is real. Don't you?
00:31:32
London Tsai: I do. I mean, as an artist, as a contemporary artist, I'm often told not to mention the math behind my work.
00:31:46
Eric Weinstein: Who told you that?
00:31:47
London Tsai: I mean, general people just say they're not interested in the math. They're not...
00:31:54
Eric Weinstein: All right, maybe you're not supposed to mention it but I'm certainly supposed to mention it.
00:31:59
London Tsai: It's—I think people, when they see that there is mathematics behind it, I think it scares them off.
00:32:06
Eric Weinstein: Yeah.
00:32:07
London Tsai: And most people have bad memories of their mathematical upbringing, or education, that they have this reflex to just turn away from it.
00:32:20
Eric Weinstein: Well it's like the bad ex-boyfriend problem, is that if you meet somebody who's had a bad relationship, they're always going to live through some of that trauma in every subsequent relationship. And I think that we have to recognize, you know, we talk about iatrogenic harm as the harm done by physicians to patients, and we have to talk about mathogenic harm, where there is this, like, destruction of the love and appreciation for the beauty of math that is mediated by math teachers, and mathematicians, and math professors.
00:32:56
Like somehow we're keeping the beauty for ourselves, and a large number of people have no idea. They've just been like—I don't know, they've had their knuckles rapped with a ruler, and they're now in some damaged state. And, I guess when you look at this stuff, some percentage of people will say, "I don't get it. It's not that interesting. It leaves me cold." Some other percentage of people are gonna look at it and say, "I've got to figure out what that was about. I didn't know that that was there."
00:33:26
London Tsai: Yeah.
00:33:31
Eric Weinstein: Are you connected with any of these people I mentioned?
00:33:36
London Tsai: You mean the people that are not—
00:33:38
Eric Weinstein: Like Bathsheba Grossman, or Cliff Stoll.
00:33:39
London Tsai: Oh no, I'm not. I'm not. No, I know who they are, yeah, yeah, yeah. I think you and Andrew had the Klein bottles during that interview.
00:33:50
Eric Weinstein: Oh, Andrew Yang.
00:33:51
London Tsai: Yeah. [Unintelligible]
00:33:51
Eric Weinstein: Yeah. So are you a Yang supporter?
00:33:55
London Tsai: Yeah.
00:33:56
Eric Weinstein: Okay. Well, so he's got these "MATH" hats, I would love to be made math czar in a coming Yang administration.
00:34:02
London Tsai: I figure I should get my hands on one.
00:34:06
Eric Weinstein: Yeah. So to some extent, this is actually not the first generation of mathematical or physical art in your family. Am I right that your father, somehow, was mining this vein as well?
00:34:24
London Tsai: Yeah. So my father trained as an engineer and worked as a mechanical engineer for 10 years, quite successfully, in New York City. And the whole time he wanted to be an artist, and he was painting at the Art Students League, and he made all these paintings, figurative, and then abstract, and so on. Then he won a prize for painting. And then, the stipulation for the prize was that he had to quit his engineering career and devote himself to art. Upon quitting, he found he couldn't paint anymore. He kind of did some soul searching, traveled around the world, and that's when he realized that there was something that he could do with his engineering background. Somehow, he could bring engineering and science into his artwork. That's when he started developing his cybernetic sculptures, and he never turned back. He always make these kinds of scientific, engineering—
00:35:35
Eric Weinstein: I just saw them for the first time at your studio. They're gorgeous. I mean, I love your stuff, and I didn't know that I was gonna love his. He had these gorgeous standing waves, and then by the use of clever use of stroboscopic light, he's able to freeze them and show this very subtle motion that would otherwise be lost. And I think that the wave equation, which is of a particular class of equations well known in mathematics, is one of the most beautiful things I've ever seen. And to be able to visualize waves is precious to me. Astounding that I wasn't aware of his work.
00:36:22
London Tsai: I think the lesson from my father—he never thought of himself as a scientist, or as a technological artist. He thought of himself just as an artist. And I think what he was trying to say with that was that technology and science, they're not really like tools, or that you could just say, "Oh, that's a technological artist." That these are just things that, as artists, that are part of our culture, part of our society, that we have a right to use them just as much as professional scientists do.
00:37:07
And I think in that way, I think of myself as an artist—not as a mathematical artist, but as an artist. And it turns out that having seen mathematics, and having been exposed to mathematics, it's just like part of humanity that I've incorporated in myself, and the artwork that I make has those features because it's my life experience. So I'm not sure that we can term this movement as mathematical art, but I think we're just artists who are expanding our understanding to those realms that are difficult for most people to reach, and I think—but that's part of what it means to be human, you know, it means to expand ourselves.
00:38:06
Eric Weinstein: We don't call—just to steelman your point—we don't call Salvador Dali a mathematical artist, and yet, if he puts Jesus on a 4-dimensional polytope in the case of a tesseract or hypercube, we just accept that he's mining some amount of mathematics as an inspiration for his art. You know, the development of the use of linear perspective wasn't viewed as mathematical art. A lot of Op art—I mean, if you think about Vasarely, I think that a lot of those patterned structures that he depicted that appear to be showing curvature by using various optical tricks—we don't call that mathematical art necessarily.
00:38:47
However, you are going beyond that, and so I don't know whether it's exactly fair to avoid the label. I mean, I'll try to come up with a better one. But, you know, I often look at my own soul—for lack of a better word—and I realize that I may not be able to believe in angels, or religious origin stories, but I still have a place in my consciousness, or my heart, or whatever you want to call it, that wants to be connected with something larger than the human experience. I don't want to just die on a random rock and having it all, as Shakespeare said, "Signifying nothing."
00:39:43
And one of the things that I actually take spiritual solace from is that at a minimum, there is this world of structures that would have passed by completely unknown, like the Hopf fibration, which was only found in the 1930's. So we have people who are alive who are older than the knowledge that the Hopf fibration exists. And these things are like angels. We know that they're there, it's not speculative. And we know that we didn't create them. And we know that they seem to be transcendent. And I would just assume, fill my life with transcendent structures that are beyond any kind of human authorship and not call—you know, I mean, the art here to me is your decision to depict this and the way in which you chose to depict it, but the source that you're mining has nothing to do with our humanity.
00:40:46
London Tsai: I see.
00:40:48
Eric Weinstein: Right? In essence, the thing that you have behind you right now is to me a modern picture of an angel, where I can't believe an angels but I can believe in principal fiber bundles generating the world of electromagnetic activity, which then grew up and not only became Maxwell's equations, became every kind of force other than gravity.
00:41:19
London Tsai: I mean, yeah, maybe math is not a product of humanity. But, I feel that the struggle to understand math, and to create these mathematical texts, I mean that in itself is us—that has a very human aspect to it. And that's one of the properties I'm trying to express in my art, is just trying to express that maybe even though math is not a human thing, somehow it's a much deeper—it's a universal thing. But that its practice is human, and that I want to show the humanness by—
00:42:08
Eric Weinstein: That's what you're doing for me, you just humanized an angel.
00:42:12
London Tsai: Yeah, I want to bring that out. It's very important that the hand of the artist be present, kind of like expressing the difficulty that as a human being I have to try to understand these things.
00:42:27
Eric Weinstein: Hell yeah. I see struggle, that I look at all of the text that's going in and around the color, or in the charcoal drawings, and I struggle to read it. It's hard to read it because it's not presented to be read in this typical fashion. And I love the fact that it is slightly irregular. And it shows, in some sense, a perfect structure that cannot be depicted perfectly.
00:42:56
London Tsai: Right. Yeah.
00:42:58
Eric Weinstein: Do you ever feel freaked out, being in direct touch with these otherworldly structures?
00:43:07
London Tsai: I feel inadequate. That no matter how much time I spend with them, there's—I can really never quite grasp it in its totality. It's somehow beyond my reach. And of course, you know, then sometimes I blame, "Oh well, maybe that's my ability. I'm just not—I just don't have"—
00:43:32
Eric Weinstein: No, I think what we have to back away from [is] how creepy it is that these things are even there to be found. You know, I typically give the example of exceptional Lie groups or exotic 7-spheres—which are structures people can look up if they dare—as things that both make me feel not alone and make me feel vaguely terrified. You know, it's like, what if a cigar-shaped object started hovering over the Earth and it didn't do anything malignant, but we knew it wasn't from us, and we didn't know what it was. It didn't show any signs of life, other than the fact that it was there.
00:44:20
London Tsai: When I was a child, I used to have dreams like that—nightmares like that. And this is long before I knew anything about math, I would dream about these huge surfaces. And I was so tiny, like the size of the ant. And they would be so smooth like infinitely smooth. I had no idea what infinitely smooth meant, but they were so smooth and they were terrifying. And maybe that's kind of like my very first kind of mathematical experience, just these things that appeared in my dreams.
How to Find London's Art[edit]
00:44:55
Eric Weinstein: Now, one of the weird things that we're doing on this podcast is we're picking on people who don't necessarily know that we're coming, and promoting what they do. And we call this reverse sponsorship. And the hope is that if we have a successful business, and we can pick on it, that as we generate interest in that business from our audience, that maybe some of those businesses will come and sponsor The Portal, and keep us on the air when we go into very difficult topics.
00:45:31
I'm not trying to ever ask that of you. But I do want to say that in some sense, this episode is part of something akin to reverse sponsorship. I think that the biggest problem—and tell me if this rings true or not—is that a lot of us do work that never gets curated by a second person. That in general, I used to think curation was a parasitic behavior. If you couldn't create, you could point things that were great. And I later realized, with my own stuff, that until somebody else said, "Hey, this person is saying something," that you don't actually get heard or processed, because you can't actually curate yourself. Somebody else has to be the pointer and saying, "Hey people, pay attention."
00:46:19
And I think it's way past time that this be done for you. I know most mathematicians don't have large audiences. This is not a field—physics has a few, tiny number of physicists who have large audiences. But I really believe that it's essential for a curation process to happen with this kind of work, so that people can see more of what is out there. Are you open for business? Will you sell your work? Are you—I found you on the internet.
00:46:52
London Tsai: Yeah, sure.
00:46:53
Eric Weinstein: Yeah?
00:46:54
London Tsai: Yeah.
00:46:57
Eric Weinstein: Okay. So hopefully, supporters of the program can look for London and his storefront on the internet somewhere. What about exhibiting with other artists, and showing this kind of new wave of whatever we want to call it other than mathematical art?
00:47:20
London Tsai: Right. Oh, I'm open to that.
00:47:22
Eric Weinstein: Oh yeah?
00:47:23
London Tsai: Absolutely.
00:47:24
Eric Weinstein: So you would do like a group show?
00:47:25
London Tsai: Yeah, of course.
00:47:28
Eric Weinstein: Are you up for like suggestions? I've been horrible to you. I've told you a bunch of things that I've never seen depicted and asked you to look in on it. Is that is that an overbearing question?
00:47:38
London Tsai: No, that's a good, that's a great—well, I did a series of talks when I lived in Seattle. So I went to University of Washington, where I knew a couple mathematicians. And it was a series of works I called Demonstrations. It was kind of inspired by da Vinci's scientific drawings, dimostrazione. And so I invited UW mathematicians to supply me with theorems of theirs, and I would attempt to come up with my own interpretation. That was that was a fun project, I got to know a few mathematicians at the UW. And yeah, that sort of collaboration was something I was very interested in, about 10 years ago.
00:48:38
Eric Weinstein: What are you thinking about now?
00:48:40
London Tsai: What am I thinking about now—I'm always open to new ideas, and your list of topics is a printout I carry with me every day, so I'm always looking at it on the subway.
00:48:50
Eric Weinstein: Really?
00:48:51
London Tsai: Yeah. Yeah. So Atiyah-Singer index theorem. Yes, I'm trying to wrap my head around that. I think you had something of a carevair, Kervaire—
00:49:07
Eric Weinstein: Kervaire invariant 1 problem.
00:49:09
London Tsai: Yes.
00:49:10
Eric Weinstein: Yeah, that's gorgeous stuff.
00:49:10
London Tsai: Yeah. So I, yeah, I look at it, and I have my mathematician friends, and I have a whole library of math textbooks that I try to consult.
Quadric Surfaces Painting[edit]
00:49:25
Eric Weinstein: So maybe—if I'm correct, the vector bundle painting that is behind me is masking another work that's underneath it. Maybe we could take the top painting off and take a look at what you have there.
00:49:41
London Tsai: Okay, sure. Let's do it.
00:49:43
Eric Weinstein: All right. So London, you've just unveiled this other structure. And I'm looking at it, and it's on its side from what I normally expect so that we can get it into the shot.
00:49:53
London Tsai: That's right. Yeah.
00:49:54
Eric Weinstein: But what it looks to me like is that you've taken the light cone, on which particles with no rest mass, or waves with no rest mass, propagate inside of the special theory of relativity, and then you sort of showed this algebraic—how do you say it, algebraic degeneration? So it looks like I'm looking at some mass shells, and this diagram that should be familiar from Einstein's famous Annus Mirabilis of 1905, when he figured out special relativity, has been sort of augmented with this extra structure of of mass shells and hyperboloids. And what can you say about what motivated you here?
00:50:51
London Tsai: Well, so I painted a painting of some of my favorite things from Calculus III, quadric surfaces. And I showed it to Loring Tu, and he said, "Well, that's very interesting, but can you tell me how they're related?" And so that was a direct challenge from Loring. So I thought about, 'Well, if I vary a certain parameter, this was what happened.' But as I went from one of these types of surfaces to the other type, from the hyperbola of two sheets to the hyperbola of one sheet, I had to go through the cone. And so I showed that relation—that was basically the idea behind that piece.
00:51:44
Eric Weinstein: It's gorgeous.
Inspirations from Nature and Music[edit]
00:51:51
Eric Weinstein: Do you find any comparable source of rich imagery from any other area other than, let's say, mathematics and physics?
00:52:10
London Tsai: I would say nature.
00:52:13
Eric Weinstein: Are you as fascinated by it?
00:52:18
London Tsai: I'm not—maybe I'm not as fascinated by it, but you know, if I'm walking on the beach and I pick up some shells—
00:52:24
Eric Weinstein: No, no, no, it's unbelievably gorgeous, but I have to admit that nature, weirdly, though it completely inspires me, and I think no less than it inspires other people, I'm weirdly slightly less inspired by physical nature than I am by what we might call mathematical nature.
00:52:44
London Tsai: I have to say I'm the same. Although I am—I'm a scuba diver, I'm a downhill skier—
00:52:52
Eric Weinstein: Yeah. But downhill skiing is pretty close to differential geometry.
00:52:55
London Tsai: Yes it is. I'm constantly thinking about the curvature of the terrain I'm on, yeah.
00:53:00
Eric Weinstein: What are you fascinated by in scuba diving?
00:53:04
London Tsai: Scuba diving, when I go down I just see the strange sea creatures residing on the ocean floor, or you know, on the coral reefs, and the shapes of them—
00:53:16
Eric Weinstein: Any particular ones you're obsessed with?
00:53:20
London Tsai: I can't say I'm obsessed about them, I just find them interesting.
00:53:24
Eric Weinstein: I thought maybe cuttlefish.
00:53:26
London Tsai: Cuttlefish?
00:53:28
Eric Weinstein: I mean, the skin of the cuttlefish is a nearly mathematical phenomenon. If you've ever watched them propagate these waves through the chromatophores on the skin, when they're mesmerizing their prey before they strike—the patterns, it's sort of like Times Square with some giant neon sign that's moving through these pulses of light.
00:53:52
London Tsai: I guess I've never seen that diving.
00:53:54
Eric Weinstein: Okay. And in music, what do you find yourself most inspired by?
00:54:05
London Tsai: I like, well, when I work in my studio I'm often listening to jazz, usually Miles Davis, Dave Brubeck, or, you know—
00:54:18
Eric Weinstein: Dave Brubeck obviously famous for experimenting with funny time signatures, which is somewhat mathematical.
00:54:24
London Tsai: I also listen to a lot of classical music.
00:54:28
Eric Weinstein: Yeah. Favorite composer?
00:54:33
London Tsai: Mozart, Rachmaninoff.
00:54:35
Eric Weinstein: Really? I never trust a mathematician who doesn't say Bach first.
00:54:39
London Tsai: Oh, Bach. That's true.
00:54:41
Eric Weinstein: Okay, well no, maybe the idea is that's not your jam when it comes to the—
00:54:45
London Tsai: No, I do love Brandenburg Concerto. I rock to that.
Other Math Public Outreach[edit]
00:54:50
Eric Weinstein: And are you at all familiar with any of these attempts to push math, and reverence for math, out to the general public that are somewhat off of the direct depiction? I don't know if you've ever seen my friend Edward Frenkel's short film Love and Math. And then he wrote a book.
00:55:15
London Tsai: No, I don't think I've seen that.
00:55:17
Eric Weinstein: It's a slightly erotic art film.
00:55:18
London Tsai: Really? Okay, no, I haven't.
00:55:22
Eric Weinstein: And I guess, you know, one of the things that I'm very frustrated by is that it's just so difficult to communicate it. A counterexample to this would be—have you ever been to the Exploratorium in San Francisco?
00:55:36
London Tsai: Yeah I have, a long time ago though. A couple of decades ago.
00:55:39
Eric Weinstein: So Frank Oppenheimer, who was Robert Oppenheimer's brother, created this totally anomalous science museum that was much more effective—so far as I could tell—in conveying the wonder of science in a way that people actually got some kind of a take home, like it was viscerally engaging. And yet, I didn't see that kind of science museum duplicated anywhere else. Might that be a paradigm where someone, somewhere, could do something truly unique with the visual depiction of geometry and topology, let's say, and completely crack this open? I mean, to take the Promethean analogy, all it really takes is one of us to steal fire, effectively.
00:56:32
London Tsai: Yeah, that might work. Have you been to the Google Math Museum in Madison Square Park?
00:56:39
Eric Weinstein: I've been to the Math Museum, is Google sponsoring it now?
00:56:43
London Tsai: I thought it was sponsored by Google, maybe I'm wrong.
00:56:44
Eric Weinstein: I didn't think it was.
00:56:45
London Tsai: Okay. I didn't know, I just assumed it was.
00:56:48
Eric Weinstein: Yeah, I thought it was somewhat inspiring, but a lot of this stuff is sort of strangely, slightly off. There's this beautiful limestone wall in Stony Brook, Long Island, that has some of the most beautiful formulas in all of mathematics and some pictures. But to me, even that has like errors and flaws, and it doesn't fully evoke what it is that it was trying to depict. I feel like we failed. What do you have—
00:57:23
London Tsai: Yeah, I feel that too. I mean, that's partially why I don't think of my art as mathematical art, because I don't want it to be associated with those kind of like, "Oh, bring math to the people," that kind of thing. It has to be somehow something—I mean, like the wonder of math that we experience, studying, that is not—I don't feel that when I go and look at these kind of displays of mathematical art. Oh, how interesting how these things fit together, and you're just like okay, let me just play with this a little bit, and then move on to this other exhibit. And here now you—
00:58:03
Eric Weinstein: What do you feel when you when you look at Escher?
00:58:09
London Tsai: I didn't—well, my initial reaction, when people were, "Oh, you're a math major, you should love Escher," I was like, "Oh, that's great."
00:58:19
Eric Weinstein: I viewed the art and the math as somehow strangely separate, and it was a great way of getting a certain amount of math out into the world. And I found him quite artistic, I just didn't feel that the art and the math were always hand in glove.
00:58:36
London Tsai: Yeah, like, well first of all, like symmetry groups of the plane, I mean that's cool. But still, there's—it doesn't capture the real depth of math. And there's just so much more to math than just pretty patterns, or symmetrical patterns.
00:58:54
Eric Weinstein: Are you obsessed with physics?
00:58:57
London Tsai: Not as much as I wish to be, yeah.
00:59:02
Eric Weinstein: I think one of the great mysteries for me has been why is it that the physical universe is such an amazing client of the best mathematics? Right? Like you could have done this with substandard mathematics, maybe just a little bit of calculus and some linear algebra, but it just goes way above and beyond, and actually uses our best stuff, and our most beautiful stuff. And I've always thought that was quite odd, that it didn't have to be the way—the biological world does not seem to use mathematics at a truly profound level. There's some cute stuff with Fibonacci sequences, but I would say that the biological world mostly turned up its nose that the mathematical offerings that that were possible.
00:59:49
London Tsai: I guess I see physics and math as so, like—
00:59:52
Eric Weinstein: Intertwined.
00:59:53
London Tsai: Intertwined, yeah.
00:59:52
Eric Weinstein: Well you know, there's this expression, "The map is not the territory," and I think that the weird thing about physics is that physics may be the one place in the real world in which the map—that is. the math that describes it—may actually be the territory. That is, it would not astound me if life really was about vector bundles, principal bundles, and wave equations that take place upon them.
01:00:17
London Tsai: Yeah.
Conclusion[edit]
01:00:19
Eric Weinstein: So, we're going to try to figure out how to get you as part of an exhibition so people can come and see your work. They can find you on the internet, you have a site?
01:00:32
London Tsai: Yeah. So my site is just londontsai.com.
01:00:36
Eric Weinstein: That's T-s-a-i?
01:00:37
London Tsai: Yeah.
01:00:48
Eric Weinstein: Okay, and first name, improbably, is London.
01:00:40
London Tsai: Yes, L-o-n-d-o-n.
01:00:42
Eric Weinstein: Yeah. And other than that, we're going to continue plugging your work, pointing people to your Instagram page, and trying to drum up some interest so that you'll make more of this gorgeous stuff for all of us.
01:00:57
London Tsai: Well thank you very much, Eric.
01:00:59
Eric Weinstein: London, it's been pleasure having you. You've been through The Portal with London Tsai. Look for him on Instagram, on Twitter, and most importantly at his website, and consider making a bid to keep me from buying this art. I think you'll find that it's just gorgeous stuff.
01:01:17
Look for us at The Portal on Apple, on Spotify, on Stitcher, wherever you listen to podcasts. Please subscribe, and go over to YouTube and see if you can subscribe to us there, and click the bell icon to make sure that you're notified when our next episode drops. Hopefully, if you've listened to this on audio, you will go over there and watch it on video so you have a little bit of a taste of the great stuff that London has been doing. London, thanks very much.
01:01:43
London Tsai: Thank you, Eric.
01:01:44
Eric Weinstein: All right everybody, be well.
Portal Player Markup[edit]

Lun-Yi London Tsai is a mathematically-trained visual artist based in Brooklyn, New York whose practice includes drawing, painting, welded metal sculpture, and kinetic sculpture.
Examples of London's work



Petra originally known to its inhabitants as Raqmu, is a historical and archaeological city in southern Jordan. Petra lies around Jabal Al-Madbah in a basin surrounded by mountains which form the eastern flank of the Arabah valley that runs from the Dead Sea to the Gulf of Aqaba.

Johannes Brahms (7 May 1833 – 3 April 1897) was a German composer, pianist, and conductor of the Romantic period. Born in Hamburg into a Lutheran family, Brahms spent much of his professional life in Vienna. His reputation and status as a composer are such that he is sometimes grouped with Johann Sebastian Bach and Ludwig van Beethoven as one of the "Three Bs" of music, a comment originally made by the nineteenth-century conductor Hans von Bülow.
The visual cortex is the primary cortical region of the brain that receives, integrates, and processes visual information relayed from the retinas. It is in the occipital lobe of the primary cerebral cortex, which is in the most posterior region of the brain.

Columbia University in the city of New York.

Heinz Hopf was a German mathematician who worked on the fields of topology and geometry.

In the mathematical field of differential topology, the Hopf fibration (also known as the Hopf bundle or Hopf map) describes a 3-sphere (a hypersphere in four-dimensional space) in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle. Technically, Hopf found a many-to-one continuous function (or "map") from the 3-sphere onto the 2-sphere such that each distinct point of the 2-sphere is mapped to from a distinct great circle of the 3-sphere (Hopf 1931). Thus the 3-sphere is composed of fibers, where each fiber is a circle — one for each point of the 2-sphere.
