Graph, Wall, Tome: Difference between revisions

From The Portal Wiki
(→‎Graph: Added missing word in Graph transcription —Aardvark)
Tags: Mobile edit Mobile web edit
 
(191 intermediate revisions by 17 users not shown)
Line 1: Line 1:
== Background ==
{{InfoboxProject
|project=Graph, Wall, Tome
|image=[[File:Ascending and Descending.jpg]]
|topic=Graph, Wall, Tome
|leader=[https://twitter.com/AardvarkLaurant Aardvark (Aardvark#5610)]<br>[https://twitter.com/Tim_Melon Tim (TimFH#7940)]
|startdate=27 January 2020
|customlabel1=<!-- Placeholder -->
|customdata1=<!-- Placeholder -->
|customlabel2=Google Drive
|customdata2=[https://drive.google.com/drive/folders/1706CBEJQEMppV60OU8OtcXxicluk2T3Y?usp=sharing Drive]
|customlabel3=Master Planning
|customdata3=[https://docs.google.com/document/d/1t9AvvFZzODw1WiGRZwRsFFZdPdBzYVJGLHiqWNrMtIA/edit?usp=sharing Doc]
|customlabel4=Reference Material
|customdata4=[https://docs.google.com/document/d/18rN-zfv41xeH3WFNOrZNb7Clz-yu1dgulP4bcEPKbcY/edit?usp=sharing Doc]
|link1title=Website
|link1=[https://graphwalltome.com/ Homepage]
|link2title=<!-- Projects Page -->
|link2=<!-- Projects Page Link -->
|link3title=
|link3=
|link4title=Discord
|link4=[https://discord.gg/Z3u3pPm Invite]
}}


Imagine:
The knowledge of fundamental physics and the mathematics necessary to perform and understand it are known to few, maybe some tens of thousands of people at most, and commitment to reach those levels entails almost a decade of graduate and post-graduate study. Yet what if it was all much easier and much harder to understand? What if the necessary knowledge was finite and more rapidly attainable to a broader population than those select few? What if there was a way to identify and abstract the most basic physical structures, a list of all the tools to build and operate on those structures, and a user's guide to describe how to use those tools?


It's 1915, and you've made one of the greatest discoveries in hundreds of years. You visit your mother and show her your work:
The '''Graph, Wall, Tome''' project demonstrates that these resources exist and already cover much of the necessary ground, but also that they are still flawed and need refinement. Edward Witten, perhaps the most intelligent living physicist, wrote a [[#Graph|paragraph]] in 1987 (from his address at the International Congress of Mathematicians, Berkeley, August 1986) that linguistically encodes and abstracts the most basic structures underlying physics, such that their function can still be understood even if the particular underlying equation may change. This is the '''Graph'''. Jim Simons, billionaire physicist, commissioned the [[#Wall|iconic Wall at State University of New York Stony Brook]] which has inscribed upon it the equations of what Witten says in addition to some of history's most important mathematical and physical results. This is the '''Wall'''. [[Sir Roger Penrose]], Nobel laureate and intellectual descendant of Albert Einstein’s school of geometric physics, wrote a book titled [[#Tome|''The Road to Reality'']], which describes and summarizes how to use the mathematics and physics contained within the Wall and the Graph. This is the '''Tome'''.


$$R_{\mu v}-\frac{1}{2}Rg_{\mu v} = 8 \pi T_{\mu v}$$
Already in these objects together is enough information to begin a serious study of physics at its most fundamental level and comprehend the deep connections between mathematics and physics. Yet, almost no one knows or seeks them. Further still, as recently as the 1950s we were confused about the structure of the universe: we didn't know the world is left-right asymmetric, as discovered by [https://en.wikipedia.org/wiki/Chien-Shiung_Wu Madame Wu], and we didn't know the [https://en.wikipedia.org/wiki/Aharonov%E2%80%93Bohm_effect Aharonov-Bohm effect], which demonstrated that the electromagnetic field is less important than the electromagnetic potential. In the mid-1970s as well, Jim Simons and C.N. Yang showed that particle theory is completely geometric. Both of these developments are little known among the public. That the Graph, the Wall, and the Tome and these recent foundational developments are unknown is evidence that something is off in how we communicate science and hand down our knowledge.


'That's nice dear', she responds, unaware of the implications of your discovery.
The aims of Graph, Wall, Tome lie in an extremely focused presentation of its core elements, improving and expanding upon the originals where necessary, to chart the path to learning fundamental physics for as many willing people as can be reached. <!-- It is not an easy road to travel, but it is one extremely rewarding, and it is the one that, in the past 100 years alone, is responsible for the comforts and relative peace we enjoy today. -->


The problem, is that although this equation carries with it the secrets of gravity, to a layman it is merely a bunch of letters.
Beyond Graph, Wall, Tome is the '''Search''', the search for a theory of everything. Ventures that may be considered part of the search are String Theory, Loop Quantum Gravity, Garrett Lisi's E8, and [[Eric Weinstein|Eric Weinstein's]] [[Theory of Geometric Unity|Geometric Unity]]. Graph, Wall, Tome can serve as a road to participate in the Search, though it should not be confused for the Search, and the Search should not be confused for it.


Now, consider this single image.
__TOC__


[[File:sheetsunx.gif||Curved Space-Time]]
=== Prime Directive ===
<blockquote style="width: 600px; text-align: center; margin-left: auto; margin-right: auto; font-size: 125%;>
A request:


Instantly, the meaning becomes clear. Gravity warps space(time), and matter, planets, and even light follows the curved path.
Try to draw the lines through the three. View it as a unified idea:


Fundamental physics is an unknown world to most people. Equations, symbols, and incomprehensible terms abound, and unless you've studied post-grad mathematics and physics, this world is inaccessible to you.
The Paragraph gets edited,


Although there are several great resources to map the way toward complete understanding. Most people will not undertake the journey to understand the source code to the world that we all inhabit.
The Wall gets defaced and graffitied,


== The GWT Project ==
The Sacred Tome gets rewritten.


Bringing an understanding of fundamental physics is one aim of The Portal.
But follow the skeins through each.


There currently exist 3 resources that themselves contain all that you need for an almost complete understanding of the world.
The Graph points to the Wall,


# The Graph - A paragraph written by Ed Witten
And the Wall to the Tome,
# The Wall - The iconic wall of Stony Brook University
# The Tome - The book 'The Road to Reality' by Roger Penrose


These resources are available to everyone, but will be sought by almost none. The aim of the GWT project to convert these resources into a medium that can be widely disseminated, and which can not be ignored.
And the Tome leads to the Search.
 
</blockquote>
This project will require bi-directional information transfer, and the minds of people with many different aptitudes.
 
* We need mathematicians, topologists, geometers, and physicists to understand these resources, and all of their implications.
* We need explainers, and educators, to convey this information to a wider audience.
* And we need artists, linguists, and programmers to create intuitive visualisations.
 
The Portal will create a community of people, working together to that achieve these aims.


Success will generate yet further insights, perhaps opening up a more fundamental understanding of the nature of reality.
=== Graph ===
The Graph is a paragraph from Edward Witten's 1987 paper [https://cds.cern.ch/record/181783/files/cer-000093203.pdf Physics and Geometry] at the bottom of page 20. In language it concisely encodes the general structure of reality:


<blockquote style="font-size: 125%;">
If one wants to summarize our knowledge of physics in the briefest possible terms, there are three really fundamental observations:


(i) Spacetime is a pseudo-Riemannian manifold <math>M</math>, endowed with a metric tensor and governed by geometrical laws.


This was first collected in a Google Doc titled [https://docs.google.com/document/d/1Bo5ny0UyC8gEHiAaDR2Al2OSGscUWPS8NFI-hvB1z4o/edit?pli=1 Graph, Wall, Tome - Problem Solving].
(ii) Over <math>M</math> is a vector bundle <math>X</math> with a non-abelian gauge group <math>G</math>.


== The Graph ==
(iii) Fermions are sections of <math>(\hat{S}_{+} \otimes V_{R}) \oplus (\hat{S}_{-} \otimes V_{\tilde{R}})</math>. <math>R</math> and <math>\tilde{R}</math> are not isomorphic; their failure to be isomorphic explains why the light fermions are light and presumably has its origins in a representation difference <math>\Delta</math> in some underlying theory.


<blockquote>
All of this must be supplemented with the understanding that the geometrical laws obeyed by the metric tensor, the gauge fields, and the fermions are to be interpreted in quantum mechanical terms.
If one wants to summarise our knowledge of physics in the briefest possible terms, there are three really fundamental observations:
 
# [https://en.wikipedia.org/wiki/Spacetime Spacetime] is a [https://en.wikipedia.org/wiki/Pseudo-Riemannian_manifold pseudo-Riemannian manifold] M, endowed with a [https://en.wikipedia.org/wiki/Metric_tensor metric tensor] and governed by [https://en.wikipedia.org/wiki/Geometry geometrical laws].
# Over M is a [https://en.wikipedia.org/wiki/Principal_bundle principal bundle] $$P_{G}$$ with a [https://en.wikipedia.org/wiki/Non-abelian_group non-abelian structure group] G.
# [https://en.wikipedia.org/wiki/Fermion Fermions] are sections of $$(\hat{S}_{+} \otimes V_{R}) \oplus (\hat{S}\_ \otimes V_{\bar{R}})$$. $$R$$ and $$\bar{R}$$ are not [https://en.wikipedia.org/wiki/Isomorphism isomorphic]; their failure to be isomorphic explains why the light fermions are light.
# Add something about Higgs
 
All of this must be supplemented with the understanding that the geometrical laws obeyed by the metric tensor, the [https://en.wikipedia.org/wiki/Introduction_to_gauge_theory gauge fields], and the fermions are to be interpreted in [https://en.wikipedia.org/wiki/Quantum_mechanics quantum mechanical] terms.
</blockquote>
</blockquote>


=== Origin ===
<div style="text-align: center">
This is a modified version of the paragraph by Edward Witten as [https://twitter.com/EricRWeinstein/status/928296366853328896?s=20 posted by Eric via Twitter].
Scan of the original paragraph:
 
[[File:The-graph.png|class=shadow|650px]]
[[file:The-graph.png|300px]]
</div>
 
Eric Weinstein suggested several alterations, that have been included above:
 
* In (ii), “vector bundle X” should be changed to principal G-bundle.
* Also in (ii), “nonabelian gauge group G” should be changed to nonabelian structure group G.
* In (iii), <math>\ R</math> and <math>\tilde R</math> should be (complex) linear representations of G and so they are not equivalent.
 
== The Wall ==
 
[[File:The-wall.png|right|400px]]
 
This image is carved into a wall at Stony Brook University. It contains many of the most fundamental equations of physics, providing a formulaic representation of all reality.
 
[http://www.math.stonybrook.edu/~tony/scgp/wall-story/wall-story.html Source]
 
Several of the equations have been identified as having direct connections to statements in 'The Graph' (identified by numbers)
 
=== Equations ===
 
'''1: Einstein's General Relativity equation:'''
: $$R_{\mu v}-\frac{1}{2}Rg_{\mu v} = 8 \pi T_{\mu v}$$
 
'''2: Maxwell's equations:'''
: $$\nabla \times \mathbf{B} = \frac{1}{c} \frac{\partial \mathbf{E}}{\partial t}$$
: $$\nabla \times \mathbf{E} = -\frac{1}{c} \frac{\partial \mathbf{B}}{\partial t}$$
: $$\nabla \cdot \mathbf{B} = 0$$
: $$\nabla \cdot \mathbf{E} = 0$$
 
'''2: Yang-Mills equations:'''
: $$d^*_A F_A \propto J$$
 
'''3: Dirac equation''':
: $$(i \not{D}_A - m)\psi = 0$$
 
'''4: Klein-Gordon equation:''' (this is not included in 'The Wall', but it has been suggested that perhaps it should have been)
: $$\frac{1}{c^2} \frac{\partial^2}{\partial t^2} \psi - \nabla^2 \psi + \frac{m^2 c^2}{\hbar^2} \psi = 0$$
 
Einstein's mass-energy equation:
: $$E = mc^2$$
 
Kepler's 2nd law:
: $$\frac{d\theta}{dt} \propto \frac{1}{r^2}$$
 
Newton's force-acceleration equation:
: $$\mathbf{F} = m\mathbf{a}$$
 
Keplers 3rd law:
: $$T^2 \propto a^3$$
 
Newtons gravitational law:
: $$F = \frac{G m_1 m_2}{r^2}$$
 
Schrodinger's equation:
: $$i \hbar \frac{\partial \psi}{\partial t} = - \frac{\hbar^2)}{2 m} \nabla^2 \psi + V \psi$$
 
Atiyah-Singer theorem:
: $$dim\, ker \not{D}_E - dim \, coker \not{D}_E = \int_M \hat{A}(M) \cdot ch(E)$$
 
Defining relation of supersymmetry:
: $$\{Q,Q\} = P$$
 
Stokes' theorem:
: $$\int_M d\omega = \int_{\partial M}\omega$$
 
The boundary of a boundary is zero:
: $$\partial\partial = 0$$
 
Heisenberg's indeterminacy relation:
: $$\Delta x \Delta p \geq \frac{\hbar}{2}$$
 
Euler's formula for Zeta-function:
: $$\sum\limits_{n=1}^{\infty} \frac{1}{n^{s}} =  \prod\limits_{p} \frac{1}{1 - \frac{1}{p^s}}$$
 
 
Eric talked about some of the important equations on the wall. There are 2 different recorded versions of the conversation if you want to listen to it.
 
== The Tome ==
 
[[File:The-tome.png|right]]
 
This book by Roger Penrose constains a comprehensive account of the physical universe.
 
To gain an understanding and intuition for the information contained in 'The Graph', and 'The Wall', reading this book will provide a great head-start.
 
 
=== Book Details ===
 
* ISBN: 978-0679776314
* [https://www.amazon.com/Road-Reality-Complete-Guide-Universe/dp/0679776311 Road to Reality by Roger Penrose (2004)]
* There appears to be a [https://www.amazon.com/Road-Reality-Complete-Guide-Universe-ebook/dp/B01BS7NTA6 Kindle Edition] that isn't available in the US. If anyone in the community has a way to get a Kindle version of the book, please add it here.
* Purchase the book somehow, then get the [https://www.academia.edu/351112/The_Road_to_Reality_Sir_Roger_Penrose pdf here]
 
== Questions ==
 
Some questions Eric posed related to the assignment:
 
=== What is $$F_A$$ geometrically? ===
[https://en.wikipedia.org/wiki/Atiyah%E2%80%93Singer_index_theorem Atiyah-Singer index theorem]
 
=== What are $$R_{\mu v}$$ and $$R$$ geometrically? ===
[https://en.wikipedia.org/wiki/Einstein_field_equations Einstein field equaitions]
Einstein’s original publication, Die Feldgleichungen der Gravitation, in English
 
==== $$R$$ ====
 
[https://www.youtube.com/watch?v=UfThVvBWZxM&t=12m6s Explanation of $$R$$]
 
$$R$$ is a scalar value, describing the "curvature of the spacetime manifold" at each point along the manifold. It's based on a concept of 'parallel transport', where you move a vector around some path on the manifold.
 
$$R$$ can be computed at each point on the manifold, and describes the difference in the vector's angle after following an infinitesimally small path around the neighborhood of that point, vs. what it was originally. The video does a great job of visualizing when and why that vector angle change would happen, with flat vs. curved manifolds.
 
In the video, they focus first on the curvature of space. Hopefully they incorporate back in curvature in time, because that's less obvious.
 
==== $$R_{\mu v}$$ ====
 
The same video then proceeds to explain $$R_{\mu v}$$. It progresses through some concepts.
 
===== Computing length in non-orthogonal bases =====
 
First, just describing the length of a vector on a curved space is hard. It is given by:
 
$$Length^{squared} = g_{11}dX^{1}dX^{1} + g_{12}dX^{1}dX^{2} + g_{21}dX^{2}dX^{1} + g_{22}dX^{2}dX^{2}$$
 
Some notes:
 
* This is not Pythagorean theorem, because $$dX^{1}$$ and $$dX^{2}$$ are not perpendicular.
* Instead, looks like a formula to get the diagonal from two opposite vertices in a parallelogram.
* If $$dX^{1}$$ and $$dX^{2}$$ are perpendicular, then $$g_{12}$$ and $$g_{21}$$ would be 0, and we would get $$Length^{squared} = g_{11}(dX^{1})^{2} + g_{22}(dX^{2})^{2}$$
* See: [https://www.youtube.com/watch?v=UfThVvBWZxM&t=14m27s the video @ 14m27s]
 
===== Computing vector rotation due to parallel transport =====


Then, they show parallel transport when following a parallelogram, but over a curved 3D manifold. To compute the vector rotation by components, they show:
Implicit in each respective section is:
# Spin-2 Force Field for Gravity, the Einstein Field Equations
# Spin-1 Vector Boson Theory, Yang-Mills-Maxwell Equations
# Spin-1/2 Matter Theory, Dirac Equation


$$dV^{1} = dX^{1}dX^{2} (V^{1}R^{1}_{112} + V^{2}R^{1}_{212} + V^{3}R^{1}_{312})$$
These are the gauge fields referred to by the last sentence.


$$dV^{2} = dX^{1}dX^{2} (V^{1}R^{2}_{112} + V^{2}R^{2}_{212} + V^{3}R^{2}_{312})$$
Note that the quantum (e.g. quantum mechanics, quantum field theory, quantum measurement, etc...) is mentioned only after the key geometric insights.


$$dV^{3} = dX^{1}dX^{2} (V^{1}R^{3}_{112} + V^{2}R^{3}_{212} + V^{3}R^{3}_{312})$$
=== Wall ===
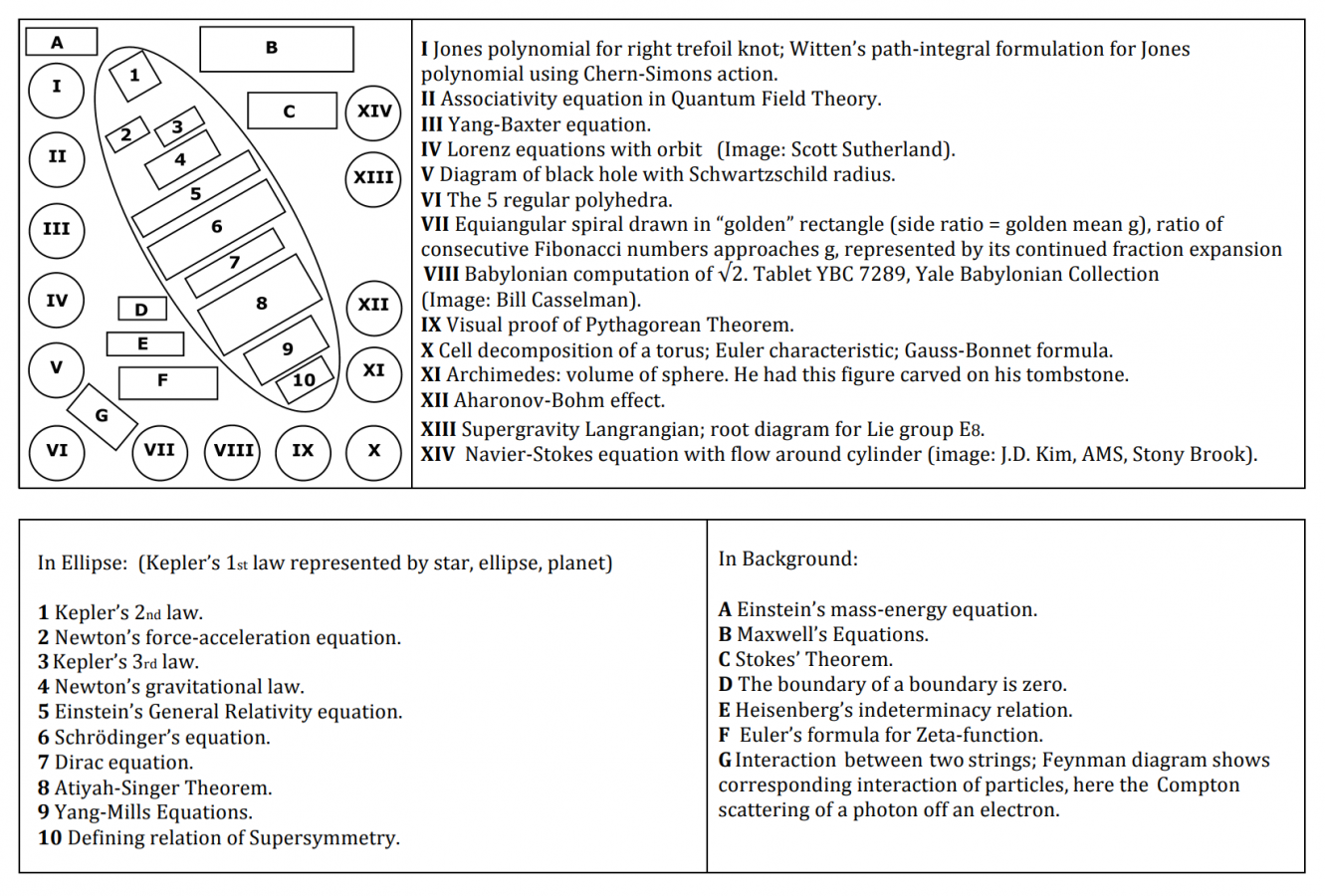
The [http://www.math.stonybrook.edu/~tony/scgp/wall-story/wall-story.html following image] is carved into a wall at Stony Brook University, completed and unveiled in May 2015. It contains many equations and mathematical results that have contributed to the human understanding of reality. In specific relation to the Graph, there are the Einstein Field Equations (item 5), the Yang-Mills Equations (item 9), and the Dirac Equation (item 7).
<div style="text-align: center;">'''[https://dev.theportal.dev/wall/ Click here for an interactive version of the Wall]'''</div>


<gallery mode="packed" heights=600px>
File:Newwall.png|center|class=shadow|400px|The Wall
File:Key-to-wall.png|center|class=shadow|800px|Legend
</gallery>


or, using $$i$$ to summarize across all 3 components (difference vectors):
=== Tome ===
{{InfoboxBook
|title=The Road to Reality
|image=[[File:The-tome.png|150px]]
|author=[[Sir Roger Penrose]]
|language=English
|genre=Physics
|publisher=Vintage
|publicationdate=9 January 2007
|pages=1136
|isbn13=978-0679776314
}}


$$dV^{i} = dX^{1}dX^{2} (V^{1}R^{i}_{112} + V^{2}R^{i}_{212} + V^{3}R^{i}_{312})$$
The Tome is ''[[The Road to Reality]]'' by Nobel laureate [[Sir Roger Penrose]], which contains a comprehensive account of the physical universe, as it was understood circa 2007, in 34 chapters spread over 1000 pages with diagrams and equations. For the information contained in the [[Graph, Wall, Tome#Graph|Graph]] and the [[Graph, Wall, Tome#Wall|Wall]], this book serves as an index of concepts to chart a path of learning. It also demonstrates how these concepts can be explained and arranged to encourage productive learning.
* [https://www.amazon.com/Road-Reality-Complete-Guide-Universe/dp/0679776311 Road to Reality by Sir Roger Penrose on Amazon]


or , using $$j$$ to index over all 3 components (original vector):
The community is reading through the tome and gathering relevant resources on the wiki.
* [https://discord.gg/3xgrNwJ The Portal Book Club] - We have a weekly group that meets to talk about this book. Come join us in Discord!
* [[The_Road_to_Reality_Study_Notes|Community study notes]]
* [[The Road to Reality|Reference material by chapter]]


$$dV^{i} = dX^{1}dX^{2} \Sigma_{j} [(V^{j}R^{i}_{j12}]$$
== Core Sub-projects ==
The essence of Graph, Wall, Tome is viewing each as part of a singular idea. What content is common among them is what should be expanded, and their unique content should be promoted if it is a part of fundamental physics toolkit, or removed if it isn't.
=== Graph-Wall-Tome Connection ===
* [[Decoding the Graph-Wall-Tome Connection]] - What are the common themes that appear in the Graph, the Wall, and the Tome? What do they point to?


See: [https://www.youtube.com/watch?v=UfThVvBWZxM&t=19m33s the video @ 19m33s]
<div class="projects-container">
{{GenericBoxWithHeader
|header=
===Editing the Graph===
|content='''[[Editing the Graph]]''' - Though the original Graph aptly summarizes our physical knowledge, there are some minor alterations and additions to be made in order for it to accurately capture current physics.}}
{{GenericBoxWithHeader
|header=
===Defacing the Wall===
|content='''[[Defacing the Wall]]''' - Update and improve the wall so that it is conciliant with fundamental theoretical physics. Remove extraneous information and reorganize to make clear the relations between underlying principles.}}
{{GenericBoxWithHeader
|header=
===Rewriting the Tome===
|content='''[[Rewriting the Tome]]''' - For everything that is in the new Graph and Wall, write their elaboration and explanation. Received wisdom does not need to be accepted wholesale, the original Tome is a good example but not the ideal solution.}}
</div>


Open questions:
=== Resources ===
* [https://docs.google.com/document/d/1t9AvvFZzODw1WiGRZwRsFFZdPdBzYVJGLHiqWNrMtIA/edit?usp=sharing Master Planning Doc]
* [https://drive.google.com/drive/folders/1706CBEJQEMppV60OU8OtcXxicluk2T3Y?usp=sharing Drive Folder]
* [https://docs.google.com/document/d/18rN-zfv41xeH3WFNOrZNb7Clz-yu1dgulP4bcEPKbcY/edit?usp=sharing List of Reference Material]


* Why a parallelogram?
== Other Sub-projects ==
* How to properly overlay the parallelogram onto the 3d manifold, in order to do the parallel transport?
* [[The Road to Reality Study Notes|Studying the Tome]] - The Tome can be intimidating. This problem can be solved 1) by creating resources that make it easier to digest its content and 2) by going through the chapters together.
* How does this relate to the length computation above?
* [[Holonomy Project]] (Stalled) - The goal is to create visualizations for the effect known as "holonomy", whereby parallel transporting a vector around a loop in a curved space leads to the vector changing upon returning to the start of the loop. How the vector changes orientation/position in space is the holonomy of that loop in that space. This effect reveals deep information about the curvature of the space itself.


== Archived Sub-projects ==
* [[Climbing the Cliff]] (Archived) - Create a learning guide through ''The Road to Reality''.
* [[Deface the Wall]] (Completed) - Cam and boqu made a new wall that's interactive.
* [[Geometry|Geometry Project]] (Archived) - The aim is to create and collect resources related to Frederic P. Schuller's lecture series titled "Lectures on Geometrical Anatomy of Theoretical Physics" that provides a great introduction to geometrical concepts that are essential for the Graph, Wall, Tome project.
* [[Interactive Wall]] (Completed) - Demp and boqu made a wall that you can pan and zoom and click on! It also pulls information from the wiki based on what is in view.


===== Putting it all together =====
== Reference ==
 
* [https://cds.cern.ch/record/181783/files/cer-000093203.pdf Physics & Geometry by Ed Witten]
Now, moving to 4D, we can compute $$R_{\mu v}$$ as:
* [http://www.math.stonybrook.edu/~tony/scgp/wall-story/wall-story.html The Wall at the Simons Center for Geometry and Physics, Stony Brook University]
 
* [https://www.amazon.com/Road-Reality-Complete-Guide-Universe/dp/0679776311 The Road to Reality by Sir Roger Penrose]
$$R_{00} = R^{0}_{000} + R^{1}_{010} + R^{2}_{020} + R^{3}_{030}$$
 
$$R_{10} = R^{0}_{100} + R^{1}_{110} + R^{2}_{120} + R^{3}_{130}$$
 
$$R_{01} = R^{0}_{001} + R^{1}_{011} + R^{2}_{021} + R^{3}_{030}$$
 
etc.
 
Indexing i over all 4 component vectors / dimensions, we get:
 
$$R_{00} = \Sigma_{i} R^{i}_{0i0}$$
 
$$R_{10} = \Sigma_{i} R^{i}_{1i0}$$
 
$$R_{01} = \Sigma_{i} R^{i}_{0i1}$$
 
etc.
 
Summarizing on $$\mu$$, we get:
 
$$R_{\mu 0} = \Sigma_{i} R^{i}_{\mu i0}$$
 
$$R_{\mu 1} = \Sigma_{i} R^{i}_{\mu i1}$$
 
etc
 
Summarizing on $$v$$, we get:
 
$$R_{\mu v} = \Sigma_{i} R^{i}_{\mu iv}$$
 
 
Open questions:
 
* If we hadn't moved from 3D to 4D, what would this all have looked like?
* What does this have to do with the parallelogram?
* Why are there two indices?
 
=== How do they relate? ===
[https://en.wikipedia.org/wiki/Cohomology Cohomologhy]
 
=== What does this have to do with Penrose Stairs? ===
* [https://en.wikipedia.org/wiki/Penrose_stairs Penrose stairs]
* [https://en.wikipedia.org/wiki/Spinor Spinor]
 
We’ve heard Eric talk about Penrose stairs and spinors - essentially phenomena where you cannot return to the original state through a 360 degree rotation, but require a 720 degree rotation.
 
=== What are “Horizontal Subspaces” and what do they have to do with Vector Potentials or Gauge fields? ===
* [https://en.wikipedia.org/wiki/Vertical_and_horizontal_bundles Vertical and horizontal bundles]
* [https://en.wikipedia.org/wiki/Introduction_to_gauge_theory Introduction to gauge theory]
* [https://en.wikipedia.org/wiki/Symmetry_(physics) Symmetry]
 
From '''theplebistocrat''':
 
<blockquote>Generally, we're wanting to understand how fermions arise from - or are embedded within / upon - topological "spaces" that have distinct rules which govern operations within those topological spaces, and then how those rules produce higher dimensional operations in corresponding spaces.
 
Just intuitively, and geometrically speaking, the image that I'm getting when describing all of this and trying to hold it in my head is the image of a sort of Penrose Tower of Babel, where the fundamental underlying structures reach upwards (but also downwards and inwards?) before reaching a critical rotation that corresponds to a collapse of structure into a higher dimensional fiber bundle.
 
But doesn't this require the symmetry break? How is left and right rotation in a subspace transformed into verticality? This is a crazy rabbit hole, friends. Keep your chins up. Let me know if this was helpful or leading astray.
</blockquote>


== Resources &amp; References ==
== Related Material ==
* [https://twitter.com/EricRWeinstein/status/928296366853328896 Eric's tweets about the Graph]
* [[20: Sir Roger Penrose - Plotting the Twist of Einstein’s Legacy|Roger Penrose on The Portal Podcast]]
* [[15: Garrett Lisi - My Arch-nemesis, Myself|Garrett Lisi on The Portal Podcast]]
* [[14: London Tsai - The Reclusive Dean of The New Escherians|London Tsai on The Portal Podcast]]
* [[A Portal Special Presentation- Geometric Unity: A First Look|Geometric Unity First Presentation]]
* [[Theory of Geometric Unity]]
* [https://www.youtube.com/watch?v=o2nG7-eXxko Eric on the Lex Fridman Podcast 134]
* [https://www.youtube.com/watch?v=rIAZJNe7YtE Eric on the Lex Fridman Podcast 88]
* [https://www.youtube.com/watch?v=wf0_nMaQ6tA Eric on JRE 1453]
* [https://www.youtube.com/watch?v=_EWCN3CPhTI Eric on JRE 1320]
* [https://www.youtube.com/watch?v=X9JLij1obHY Eric on JRE 1203]
* [https://www.youtube.com/watch?v=CJx3gLkebIA Theories of Everything on PBS Space Time]
* [https://www.youtube.com/watch?v=OI0AZ4Y4Ip4 Eric and Stephen Wolfram with Brian Keating on Into the Impossible]
* [https://www.youtube.com/watch?v=YjsPb3kBGnk Eric on Into the Impossible]
* [https://youtu.be/57SMQj3lOm0?t=4376 Into the Impossible – Sir Roger Penrose: Conformal Cyclic Cosmology, Black Holes Nobel Prize w/ Eric Weinstein Janna Levin]
* [https://www.youtube.com/watch?v=DvPvFDF9dAE Into the Impossible - Eric Weinstein: Imposter Syndrome, Donald Trump, & the Future of Theoretical Physics]
[[Category:Graph, Wall, Tome]]
[[Category:Projects]]
[[Category:Requested Project]]


* [https://drive.google.com/drive/u/1/folders/1yPZHTNy47jUpmD-RMRCVtitfD-gQBRhP Folder for Project - Graph Wall Tome]
{{SHORTDESC:A holistic view of math and physics}}
* [https://www.dropbox.com/s/xdickldblj574mf/eric%20wall%20-%20tome%20-%20graph.m4a?dl=0 Recording of original call w/ Eric]
* <span class="highlight">[[Eric’s Most Important Set of Books]]<span>

Latest revision as of 16:20, 26 August 2024

Graph, Wall, Tome
Ascending and Descending.jpg
Information
Topic Graph, Wall, Tome
Leader Aardvark (Aardvark#5610)
Tim (TimFH#7940)
Start Date 27 January 2020
Google Drive Drive
Master Planning Doc
Reference Material Doc
Links
Website Homepage
Discord Invite
All Projects

The knowledge of fundamental physics and the mathematics necessary to perform and understand it are known to few, maybe some tens of thousands of people at most, and commitment to reach those levels entails almost a decade of graduate and post-graduate study. Yet what if it was all much easier and much harder to understand? What if the necessary knowledge was finite and more rapidly attainable to a broader population than those select few? What if there was a way to identify and abstract the most basic physical structures, a list of all the tools to build and operate on those structures, and a user's guide to describe how to use those tools?

The Graph, Wall, Tome project demonstrates that these resources exist and already cover much of the necessary ground, but also that they are still flawed and need refinement. Edward Witten, perhaps the most intelligent living physicist, wrote a paragraph in 1987 (from his address at the International Congress of Mathematicians, Berkeley, August 1986) that linguistically encodes and abstracts the most basic structures underlying physics, such that their function can still be understood even if the particular underlying equation may change. This is the Graph. Jim Simons, billionaire physicist, commissioned the iconic Wall at State University of New York Stony Brook which has inscribed upon it the equations of what Witten says in addition to some of history's most important mathematical and physical results. This is the Wall. Sir Roger Penrose, Nobel laureate and intellectual descendant of Albert Einstein’s school of geometric physics, wrote a book titled The Road to Reality, which describes and summarizes how to use the mathematics and physics contained within the Wall and the Graph. This is the Tome.

Already in these objects together is enough information to begin a serious study of physics at its most fundamental level and comprehend the deep connections between mathematics and physics. Yet, almost no one knows or seeks them. Further still, as recently as the 1950s we were confused about the structure of the universe: we didn't know the world is left-right asymmetric, as discovered by Madame Wu, and we didn't know the Aharonov-Bohm effect, which demonstrated that the electromagnetic field is less important than the electromagnetic potential. In the mid-1970s as well, Jim Simons and C.N. Yang showed that particle theory is completely geometric. Both of these developments are little known among the public. That the Graph, the Wall, and the Tome and these recent foundational developments are unknown is evidence that something is off in how we communicate science and hand down our knowledge.

The aims of Graph, Wall, Tome lie in an extremely focused presentation of its core elements, improving and expanding upon the originals where necessary, to chart the path to learning fundamental physics for as many willing people as can be reached.

Beyond Graph, Wall, Tome is the Search, the search for a theory of everything. Ventures that may be considered part of the search are String Theory, Loop Quantum Gravity, Garrett Lisi's E8, and Eric Weinstein's Geometric Unity. Graph, Wall, Tome can serve as a road to participate in the Search, though it should not be confused for the Search, and the Search should not be confused for it.

Prime Directive[edit]

A request:

Try to draw the lines through the three. View it as a unified idea:

The Paragraph gets edited,

The Wall gets defaced and graffitied,

The Sacred Tome gets rewritten.

But follow the skeins through each.

The Graph points to the Wall,

And the Wall to the Tome,

And the Tome leads to the Search.

Graph[edit]

The Graph is a paragraph from Edward Witten's 1987 paper Physics and Geometry at the bottom of page 20. In language it concisely encodes the general structure of reality:

If one wants to summarize our knowledge of physics in the briefest possible terms, there are three really fundamental observations:

(i) Spacetime is a pseudo-Riemannian manifold [math]\displaystyle{ M }[/math], endowed with a metric tensor and governed by geometrical laws.

(ii) Over [math]\displaystyle{ M }[/math] is a vector bundle [math]\displaystyle{ X }[/math] with a non-abelian gauge group [math]\displaystyle{ G }[/math].

(iii) Fermions are sections of [math]\displaystyle{ (\hat{S}_{+} \otimes V_{R}) \oplus (\hat{S}_{-} \otimes V_{\tilde{R}}) }[/math]. [math]\displaystyle{ R }[/math] and [math]\displaystyle{ \tilde{R} }[/math] are not isomorphic; their failure to be isomorphic explains why the light fermions are light and presumably has its origins in a representation difference [math]\displaystyle{ \Delta }[/math] in some underlying theory.

All of this must be supplemented with the understanding that the geometrical laws obeyed by the metric tensor, the gauge fields, and the fermions are to be interpreted in quantum mechanical terms.

Scan of the original paragraph: The-graph.png

Implicit in each respective section is:

  1. Spin-2 Force Field for Gravity, the Einstein Field Equations
  2. Spin-1 Vector Boson Theory, Yang-Mills-Maxwell Equations
  3. Spin-1/2 Matter Theory, Dirac Equation

These are the gauge fields referred to by the last sentence.

Note that the quantum (e.g. quantum mechanics, quantum field theory, quantum measurement, etc...) is mentioned only after the key geometric insights.

Wall[edit]

The following image is carved into a wall at Stony Brook University, completed and unveiled in May 2015. It contains many equations and mathematical results that have contributed to the human understanding of reality. In specific relation to the Graph, there are the Einstein Field Equations (item 5), the Yang-Mills Equations (item 9), and the Dirac Equation (item 7).

  • The Wall

    The Wall

  • Legend

    Legend

Tome[edit]

The Road to Reality
The-tome.png
Information
Author Sir Roger Penrose
Language English
Genre Physics
Publisher Vintage
Publication Date 9 January 2007
Pages 1136
ISBN-13 978-0679776314

The Tome is The Road to Reality by Nobel laureate Sir Roger Penrose, which contains a comprehensive account of the physical universe, as it was understood circa 2007, in 34 chapters spread over 1000 pages with diagrams and equations. For the information contained in the Graph and the Wall, this book serves as an index of concepts to chart a path of learning. It also demonstrates how these concepts can be explained and arranged to encourage productive learning.

The community is reading through the tome and gathering relevant resources on the wiki.

Core Sub-projects[edit]

The essence of Graph, Wall, Tome is viewing each as part of a singular idea. What content is common among them is what should be expanded, and their unique content should be promoted if it is a part of fundamental physics toolkit, or removed if it isn't.

Graph-Wall-Tome Connection[edit]

Editing the Graph

Editing the Graph - Though the original Graph aptly summarizes our physical knowledge, there are some minor alterations and additions to be made in order for it to accurately capture current physics.

Defacing the Wall

Defacing the Wall - Update and improve the wall so that it is conciliant with fundamental theoretical physics. Remove extraneous information and reorganize to make clear the relations between underlying principles.

Rewriting the Tome

Rewriting the Tome - For everything that is in the new Graph and Wall, write their elaboration and explanation. Received wisdom does not need to be accepted wholesale, the original Tome is a good example but not the ideal solution.

Resources[edit]

Other Sub-projects[edit]

  • Studying the Tome - The Tome can be intimidating. This problem can be solved 1) by creating resources that make it easier to digest its content and 2) by going through the chapters together.
  • Holonomy Project (Stalled) - The goal is to create visualizations for the effect known as "holonomy", whereby parallel transporting a vector around a loop in a curved space leads to the vector changing upon returning to the start of the loop. How the vector changes orientation/position in space is the holonomy of that loop in that space. This effect reveals deep information about the curvature of the space itself.

Archived Sub-projects[edit]

  • Climbing the Cliff (Archived) - Create a learning guide through The Road to Reality.
  • Deface the Wall (Completed) - Cam and boqu made a new wall that's interactive.
  • Geometry Project (Archived) - The aim is to create and collect resources related to Frederic P. Schuller's lecture series titled "Lectures on Geometrical Anatomy of Theoretical Physics" that provides a great introduction to geometrical concepts that are essential for the Graph, Wall, Tome project.
  • Interactive Wall (Completed) - Demp and boqu made a wall that you can pan and zoom and click on! It also pulls information from the wiki based on what is in view.

Reference[edit]

Related Material[edit]


Retrieved from "https://theportal.wiki/index.php?title=Graph,_Wall,_Tome&oldid=20496"