Geometry
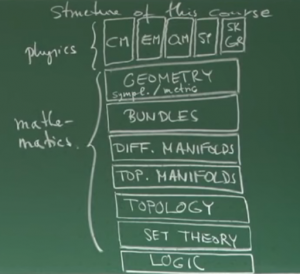
Each section corresponds to a video in the lecture series below. The pedagogy follows a conceptual stack of layered mathematical structure from first principles. The initial utility of this page is that it will ideally allow for a user to ctrl-f any technical term and find out:
- at what point it lies in the stack
- what concepts lie below it
Core lecture series: Lectures on Geometrical Anatomy of Theoretical Physics
Blogpost from which section descriptions are taken: Blogpost
High quality notes to accompany the lecture series: Simon Rea's Notes
LogicEdit
Introduction to logic; propositions and predicates; truth tables; tautologies and contradictions; negation, and, or, implication, nand connectives; existential and universal quantifiers, logical equivalence of propositions; negation of quantifiers; order of quantifiers; axiomatic systems; formal proofs; consistency and completeness.
Set theoryEdit
epsilon-relation (member relation); Zermelo-Fraenkel axioms of set theory; Russel's paradox; existence and uniqueness of the empty set (standard textbook proof and formal proof); axioms on the existence of pair sets and union sets; examples; finite unions; functional relation and image; principle of restricted and universal comprehension; axiom of replacement; intersection and relative complement; power sets; infinity; the sets of natural and real numbers; axiom of choice; axiom of foundation.
definition of maps (or functions) between sets; structure-preserving maps; identity map; domain, target and image; injective, surjective and bijective maps; isomorphic sets; classification of sets: finite and countably and uncountably infinite; cardinality of a set; composition of maps; commutative diagrams; proof of associativity of composition; inverse map; definition of pre-image and properties of pre-images (with proof); equivalence relations: reflexivity, symmetry, transitivity; examples; equivalence classes and quotient set; well-defined maps; construction of ℕ, ℤ, ℚ, ℝ (natural, integer, rational and real numbers); successor and predecessor maps; nth power set; addition and multiplication of numbers; canonical embeddings.
Topological spacesEdit
topologies and topological spaces; examples; chaotic and discrete topologies; coarser (or weaker) and finer (or stronger) topologies; open subsets; open balls; standard topology on R^d with proof; induced (or subset) topology with proof; product topology; sequences, converge and limit points; open neighbourhoods; definitely constant sequences; continuity of maps between topological spaces; examples; homeomorphisms and homeomorphic spaces.
Separations properties: T1, T2 (Hausdorff), T2 an a half; covers and open covers, subcovers and finite subcovers; compact spaces; Heine-Borel theorem (compact if and only if closed and bounded); open and locally finite refinements; paracompactness; metrisable spaces and Stone's theorem; long line (or Alexandroff line); partition of unity subordinate to an open cover; examples; connectedness and proof that M is connected if and only if M and the empty set are the only subsets which are both open and closed; path-connectedness and proof that path-connectedness implies connectedness; homotopic curves on a topological space; concatenation of curves; fundamental group; group isomorphism; topological invariants and classification of topological spaces; examples: 2-sphere, cylinder, 2-torus.
Topological manifoldsEdit
topological manifolds; manifold dimension; submanifolds; product manifold; bundles of topological manifolds; Möbius strip; total space, base space, projection map and fibres; product bundles; fibre bundles; examples; (cross-) section of a bundle; subbundles and restricted bundles; bundle morphisms and isomorphisms; local bundle isomorphisms; trivial and locally trivial bundles; pull-back of a bundle; sections on a bundle pull back to the pull-back bundle; charts, component and coordinate functions; atlases and C^0-compatibility; chart transition maps; maximal atlases.
Differentiable structuresEdit
refining a maximal atlas; C^k and smooth compatibility of charts; Cauchy-Riemann equations; differentiable atlas; compatibility of differentiable atlases; examples; proof of well-definedness of the definition of differentiability of maps; smooth maps and diffeomorphisms; diffeomorphic manifolds; classification of smooth structure on manifolds; Betti numbers.
Tensor space theory: over a fieldEdit
algebraic fields; vector spaces over an arbitrary field; vector (or linear) subspaces; linear maps; linear isomorphisms and isomorphic vector spaces; Hom-spaces; endomorphisms and automorphisms; dual vector space and linear functionals (covectors/one-forms); bilinear and multilinear maps; tensors and tensor product; examples; equivalence of endomorphisms and (1,1)-tensors; Hamel bases; linear independence and spanning set; dimension; double dual; dual bases and isomorphism of a vector space and its dual in finite dimensions; components of vectors and tensors; change of basis formulas; Einstein's summation convention and examples; column and row vectors and matrices; change of components under a change of basis; bilinear forms; permutations, symmetric group, transpositions, and signature of a transposition; totally anti-symmetric tensor; n-forms; volume-form and volume; determinant of an endomorphism.
Tangent vector spacesEdit
the space of smooth maps on a manifold; smooth curves on a manifold; directional derivative operator; tangent vectors at a point and tangent space at a point; proof that the sum of tangent vectors is a tangent vector; alternative definitions of tangent space (via equivalence classes of smooth curves, derivations at a point on germs of functions, and physical tangent vectors); algebras over an algebraic field; associative, unital and commutative algebras; Lie algebras, Lie bracket and Jacobi identity; commutator; derivations on an algebra; detailed examples; proof that derivations on a algebra constitute a Lie algebra; proof of equality of manifold dimension and tangent space dimension: dim M = dim TpM; coordinate-induced basis of tangent spaces; change of coordinates under a change of coordinate-induced bases.
Tangent bundleEdit
cotangent space and tensor space at a point of a manifold; differential of a smooth map; gradient of a real function on a manifold; dual coordinate-induced basis and gradients of coordinate functions; push-forward and pull-back of smooth maps at a point; push-forward of tangent vectors and pull-back of covectors; immersions and immersed submanifolds; embedding and embedded submanifolds; Whitney's theorem; definition of tangent bundle; proof that the tangent bundle is a smooth manifold.
Tensor space theory: over a ringEdit
vector fields as smooth sections of the tangent bundle; vector fields as linear maps on the space of smooth maps; push-forward of a smooth map as a map between tangent bundles; push-forward of a vector field; structure of the set of vector fields; rings: commutative, unital and division (or skew) rings; examples; modules of a unital ring; examples of modules admitting and not admitting a basis; Zorn's lemma; partial orders and partially ordered sets (posets); total order and totally ordered sets; upper bounds; proof that every module over a division ring (and hence every vector space) admits a Hamel basis; direct sum of modules; finitely generated, free and projective modules; homomorphism of modules (or linear maps); Serre-Swan-et al.'s theorem; pull-back of forms; tensor fields as multilinear maps; tensor product of tensor fields.
Grassmann algebra and deRham cohomologyEdit
differential n-forms; orientable manifolds; degree of a differential form; pull-back of a differential form; wedge (or exterior) product of differential forms; local expression of a differential form; proof that the pull-back distributes over the wedge product; Grassmann algebra; Grassmann numbers; proof that the wedge product is graded commutative; exterior derivative; Lie bracket (or commutator) of vector fields; example: exterior derivative of a differential one-form; proof that the exterior derivative is graded additive; commutation of the exterior derivative with the pull-back; Maxwell's electrodynamics and Maxwell's equations expressed using differential forms; symplectic forms and classical mechanics; closed and exact forms; proof that d^2=0; symmetrisation and anti-symmetrisation of indices with examples; every exact form is closed; kernel and image of a linear map; Z^n and B^n; Poincaré lemma; cohomology groups.
Lie groups and their Lie algebrasEdit
Lie groups; dimension of a Lie group; examples of Lie groups: n-dimensional translation group, unitary group U(1), general linear GL(n,R), orthogonal group O(p,q); pseudo-inner products on a vector space; Lie group homomorphism and isomorphism; proof that the left translation map is a diffeomorphism; push-forward of the left translation map; left-invariant vector fields; proof that the space of left-invariant vector fields is isomorphic to the tangent space at the identity; proof that the left-invariant vector fields form a Lie algebra, the Lie algebra of the Lie group. Lie algebra homomorphisms and isomorphic Lie algebras.
Classification of Lie algebras and Dykin diagramsEdit
complex Lie algebras; abelian Lie algebras; the trivial Lie algebra; ideal of a Lie algebra; trivial ideals; simple and semi-simple Lie algebras; derived subalgebra; solvability; direct and semi-direct sum of Lie algebras; Levi's theorem on the decomposition of finite-dimensional complex Lie algebras; adjoint map and ad; proof that ad is a Lie algebra homomorphism; Killing form; proof of the invariance (or associativity, or anti-symmetry) of the Killing form; a Lie algebra is semi-simple if and only if the Killing is non-degenerate; structure constants; components of adjoint maps and the Killing form in terms of the structure constants; Cartan subalgebra, rank of a Lie algebra and Cartan-Weyl basis; roots and fundamental roots; proof that the restriction of the Killing form on a Cartan subalgebra is a pseudo inner product; real inner product; length and angle between roots; Weyl transformations and Weyl group; Cartan matrix; bond number; Dynkin diagrams and classification of finite-dimensional semi-simple complex Lie algebras.
Lie group SL(2,C) and its algebraEdit
the complex special linear group SL(2,C): as a set, as a group, as a topological space, as a topological manifold, as a complex differentiable manifold, as a Lie group; the Lie algebra sl(2,C) of the Lie group SL(2,C); detailed calculation of the structure constants of sl(2,C); determination of the Lie bracket between left-invariant vector fields on SL(2,C).
Dykin diagrams from Lie algebras and vice versaEdit
proof that sl(2,C) is simple; Cartan subalgebra of sl(2,C); roots and fundamental roots of sl(2,C); the Dynkin diagram of sl(2,C); the A2 Dynkin diagram; detailed reconstruction of A2 from its Dynkin diagram.
Representation theory of Lie groups and their algebrasEdit
representations of a Lie algebras; representation spaces and dimension of a representation; examples of representations; homomorphism and isomorphism of representations; trivial and adjoint representations; faithful representations; direct sum and tensor product representations; invariant subspaces, reducible and irreducible representations; highest weights; Killing form associated to a representation; Casimir operator; proof that the Casimir operator commutes with the representation; Schur's lemma; worked examples; automorphism group; representation of Lie groups; Adjoint representation.
Reconstruction of a Lie group from its algebraEdit
integral curves to a vector field; maximal integral curves; complete vector fields; every vector field on a compact manifold is complete; exponential map; the image of exp is the connected component of the Lie group containing the identity; examples: orthogonal group, special orthogonal group; (restricted) Lorentz group: proper/improper orthochronous/non-orthochronous transformations; Lorentz algebra; one-parameter subgroups; flow of a vector field; the exponential map commutes with smooth maps.
Principal fibre bundlesEdit
left and right Lie group actions; example: actions from representations; proof: right actions from left actions; equivariance of smooth maps; orbits, orbit space and stabilisers; free and transitive actions; examples; smooth and principal bundles; detailed example: the frame bundle; principal bundle morphisms and isomorphisms (or diffeomorphisms); trivial bundles; proof that a bundle is trivial if and only if it admits a global section.
Associated fiber bundlesEdit
associated fibre bundle to a principal bundle; detailed example: the frame bundle; scalar and tensor densities on a manifold; associated bundle maps and isomorphisms; trivial associated bundles; restrictions and extensions of a principal bundle; examples.
Connections and 1formsEdit
vertical and horizontal subspaces at a point; decomposition in vertical and horizontal parts; connection on a principal bundle; connection one-form; properties of connection one-forms with proof.
Local representations of a connection on the base manifold: Yang-Mills fieldsEdit
Yang-Mills field as pull-back of a connection one form along a local section; local trivialisations of a principal bundle; local representation of a connection one-form; Maurer-Cartan form; example: the Yang-Mills fields on the frame bundle, Christoffel symbol; example: calculation of the Maurer-Cartan form of the general linear group GL(n,R); patching Yang-Mills fields on different domains; the gauge map; example: the gauge map on the frame bundle.
Parallel transportEdit
horizontal lifts of a curve to the principal bundle; ODE characterising horizontal lifts; explicit solution in the case of a matrix Lie group; path-ordered exponential; parallel transport map; loops and holonomy groups; horizontal lifts to the associated bundle; parallel transport map on the associated bundle; covariant derivative of a section.
Curvature and torsion on principal bundlesEdit
exterior covariant derivative; curvature two-form; characterisation of the curvature two-form with proof; Yang-Mills field strength; First Bianchi identity; solder (ing) form; torsion two-form; Second Bianchi identity
Covariant derivativesEdit
proof of the equivalence of local sections and G-equivariant functions; linear actions on associated vector fibre bundles; matrix Lie group; construction of the covariant derivative for local sections on the base manifold.