Theory of Geometric Unity
The Theory of Geometric Unity is an attempt by Eric Weinstein to produce a unified field theory by recovering the different, seemingly incompatible geometries of fundamental physics from a general structure with minimal assumptions. For the latest public updates on the theory, visit https://geometricunity.org/.
- The video presentation of Geometric Unity containing the 2013 Oxford Lecture recording is available here:
- A transcript of the talk is available here.
- Discussion on the Joe Rogan Experience Ep 1453 here.
- Discussion on PBS SpaceTime here
- Geometric Unity Predictions
- You Know You’re in GU When
The source code of the universe is overwhelmingly likely to determine a purely geometric operating system written in a uniform programming language.
- Eric Weinstein
Some Key Ideas
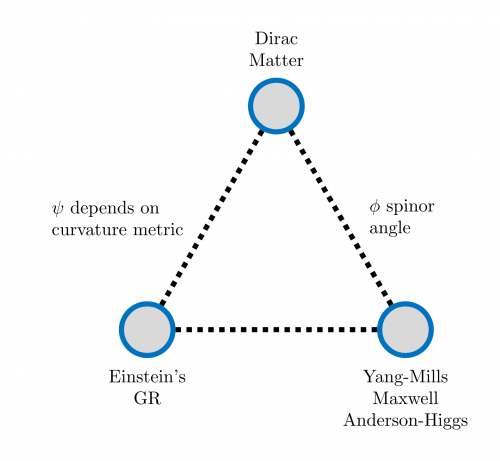
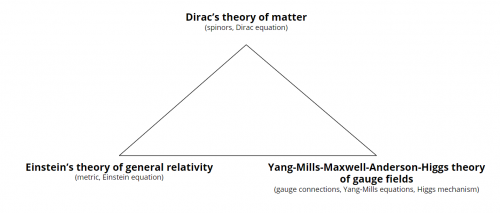
Starting point: three observations by Edward Witten
| 1. The Arena ([math]\displaystyle{ X, g_{\mu\nu} }[/math]) | [math]\displaystyle{ R_{\mu\nu} - \frac{1}{2} Rg_{\mu\nu} + \Lambda g_{\mu\nu} = \left( \dfrac{8 \pi G}{c^4} T_{\mu\nu}\right) }[/math] | the Einstein field equations, which describe gravity in the theory of general relativity |
| 2. [math]\displaystyle{ G }[/math] (non abelian)
[math]\displaystyle{ SU(3) \times SU(2) \times U(1) }[/math] |
[math]\displaystyle{ d_A^*F_A=J(\psi) }[/math] | the Yang-Mills equation, which governs all other force fields in Yang-Mill-Maxwell theory |
| 3. Matter
Antisymmetric, therefore light |
[math]\displaystyle{ (i \hbar \gamma^\mu \partial_\mu - m) \psi = 0 }[/math] | the Dirac equation, the equation of motion describing matter particles, or fermions |
Key guiding question: what are the compatibilities and incompatibilities between these puzzle pieces on the geometric level before the theory is created quantum mechanical.
Problem Nr. 1: Einstein's Theory of General Relativity is not a proper Gauge Theory
- From Einstein's general relativity, we take the Einstein projection of the curvature tensor of the Levi-Civita connection [math]\displaystyle{ \nabla }[/math] of the metric [math]\displaystyle{ P_E(F_{\nabla}) }[/math]
- From Yang-Mills-Maxwell-Anderson-Higgs theory of gauge fields, we take the adjoint exterior derivative coupled to a connection [math]\displaystyle{ d^\star_A F_A }[/math]
Idea: What if the [math]\displaystyle{ F }[/math]'s are the same in both contexts?
Further, supposing these [math]\displaystyle{ F }[/math]'s are the same, then why apply two different operators?
Thus the question becomes: Is there any opportunity to combine these two operators?
A problem is that the hallmark of the Yang-Mills theory is the freedom to choose the data, the internal quantum numbers that give all the particles their personalities beyond the mass and the spin. We can allow the gauge group of symmetries to act on both sides of the equation, but the key problem is that: [math]\displaystyle{ P_E(F_{\nabla h}) \neq h^{-1} P_E(F_{\nabla}) h }[/math]. If we act on connections on the right and then take the Einstein projection, this is not equal to first taking the projection and then conjugating with the gauge action. The gauge rotation is only acting on one of the two factors. Yet the projection is making use of both of them. So there is a fundamental incompatibility in the claim that Einstein's theory is a gauge theory relies more on analogy than an exact mapping between the two theories.
Problem Nr. 2: Spinors are sensitive to the metric
Observation: Gauge fields do not depend on the existence of a metric. One-forms are defined whether or not a metric is present. But for spinors (fermion fields) this is not the case.
"So if we're going to take the spin-2 [math]\displaystyle{ G_{\mu\nu} }[/math] field to be quantum mechanical, if it blinks out and does whatever the quantum does between observations. In the case of the photon, it is saying that the waves may blink out, but the ocean need not blink out. In the case of the Dirac theory, it is the ocean, the medium, in which the waves live that becomes uncertain itself. So even if you're comfortable with the quantum, to me, this becomes a bridge too far. So the question is: "How do we liberate the definition?" How do we get the metric out from its responsibilities? It's been assigned far too many responsibilities. It is responsible for a volume form; for differential operators; it's responsible for measurement; it's responsible for being a dynamical field, part of the field content of the system."
Problem Nr. 3: The Higgs field introduces a lot of arbitrariness
"The Dirac field, Einstein's field, and the connection fields are all geometrically well-motivated but we push a lot of the artificiality that we do not understand into the potential for the scalar field that gives everything its mass. We tend to treat it as something of a mysterious fudge factor. So the question is, if we have a Higgs field: "why is it here and why is it geometric?""
Proposed Solution
We may have to generalize all three vertices before we can make progress. That's daunting because in each case, it would appear that we can make an argument that the three vertices are already the simplest possible theories that could live at these vertices.
- We know, for example, the Dirac operator is the most fundamental of all the elliptic operators and Euclidean signature generating all of the Atiyah-Singer theory.
- We know that Einstein's theory describes, in some sense, a unique spin two massless field capable of communicating gravity, which can be arrived at from field-theoretic rather than geometric consideration.
- In the Yang-Mills case, it can also be argued that the Yang-Mills theory is the simplest theory that we can write down. In the Yang-Mills case, we have no substructure, and so we're doing the most simple-minded thing we can do by taking the norm-squared of the curvature and saying whatever the field strength is, let's measure that size.
So if each one of these is simplest possible, doesn't Occam’s razor tell us that if we wish to remain in geometric field theory, that we've already reached bottom?
I would say that there are other possibilities that while each of these may be simplest in its category, they are not simplest in their interaction.
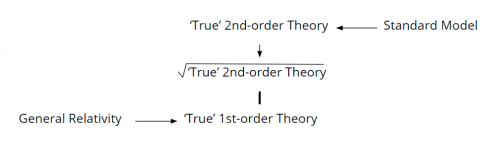
For example, we know that Dirac famously took the square root of the Klein-Gordon equation to achieve the Dirac equation. He actually took two square roots, one of the differential operator, and another of the algebra on which it acts. But could we not do the same thing by re-interpreting what we saw in Donaldson theory and Chern-Simons theory and finding that there are first-order equations that imply second-order equations that are nonlinear in the curvature?
So, let's imagine the following: we replaced the standard model with a true second-order theory. We imagine the general relativity is replaced by a true first-order theory. And then we find that the true second-order theory admits of a square root and can be linked with the true first order theory.
This would be a program for some kind of unification of Dirac's type, but in the force sector. The question is, "does this really make any sense? Are there any possibilities to do any such thing?"
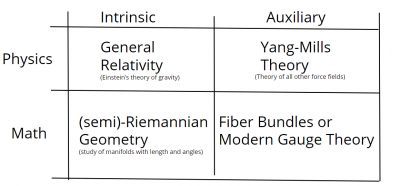
Let's talk about what the Geometric Unity (GU) proposal is. First of all, we observe that we have a division into intrinsic theories and auxiliary theory and between physics and mathematics. An intrinsic physical theory would be general relativity. An auxiliary physical theory would be the Yang-Mills theory, with the freedom to choose internal quantum numbers.
At the mathematical level, an intrinsic theory would be, the older semi-Riemannian geometry. The study of manifolds with length and angle. Auxiliary geometry is what we're going to call fiber bundle theory or modern gauge theory.
Geometric Unity is the search for some way to break down the walls between these four boxes.
What we'd like to come up with is some theory that is intrinsic, but allows us to play some of the games that exist in other boxes. How can we fit? How can we try to have our cake and eat it too? And use all the full suite of techniques that are available to us?
Our perspective is that the quantum that may be the comparatively easy part and that the unification of the geometry, which has not occurred, may be what we're being asked to do.
More about Geometric Unity on YouTube
On X
2009
New Topic:"A well meaning amateur predicts LHC Era Physics from Hedge Fund-Land." or "Why don't our pros have more interesting guesses?" #GU
GU: Two theories will gain explaining the 3 families. The one I like less will involve triality and large exceptional groups (a la Lisi).
GU: This triality family theory will be based on reps. of dim. 3*8*(2^i) for i =0,1,2,3 for F4,E6,E7,E8, ..... which don't fully exist yet.
GU: We will solve this by refining our notion of a "defining representation" to include 'projective' reps. that *cannot* be deprojectivized.
GU: I predict that it isn't *yet* game over for family triality but @garrettlisi must abandon the 26,27,78,248 'defining reps' of F4,E6-E8.
GU: This is an undervalued program to answer the generalized "Who ordered that" question of I. Rabi. ... but one still unlikely to work.
GU: Pause.
[Next: A more hopeful guess for explaining the family structure and what is next in fermion land.]
GU: [Resume.] While family triality is intriguing, I posit there is a more likely geometric basis for the 3 family structure. Here goes....
GU: I posit LHC-Era physics will come to be dominated by an N*(3+1) family structure model where the 4th family are 'black sheep' fermions.
GU: Were my model valid, 3*N would be the natural number of broken families of *spinorial* matter with N=1 the most natural value.
GU: But for every 3 spinorial families of 16 particles each, there should be a black sheep family of particles which transform differently.
GU: These black sheep particles would instead transform in the so-called Cartan product of the vector and spinorial represenations.
GU: But these particles wouldn't carry internal quantum numbers of Bosonic type. Instead, they would carry the familiar 16D rep of Spin(10).
GU: I'm looking for 144_Spin(10) new Spin 1/2 and 16_Spin(10) new Spin 3/2 fundamental fermions. The 16 wouldn't be dark. The 144 could be.
2010
GU: It is worth predicting now that a different spin 0 fundamental field will indeed show up, only to be mis-welcomed...as a "Trojan Higgs."
GU: Don't conflate Spin 0 fields valued in the adjoint bundle / non-linear sigma models w/ higgs at LHC. Nature uses Spin 0 alternatively.
2013
Marcus has asked me to delay my return to the US. I will be giving a talk on Geometric Unity for the 3rd time. Some ground rules to follow.
Just gave my Geometric Unity talk to a fairly full Oxford auditorium. The audience was terrific w/ great questions from the physicists. Thx!
2014
Geometric Unity contrasted w/ M-theory over at @edge in my answer to the annual question. #edgeQ What's your choice? https://t.co/touzrIa0aj
2016
Just gave my 1st talk on my Geometric Unity thy in over 3 years in private breakaway session @ #FQXi2016! Three tough minds asked great Qs.
2017
@ChaosRapist Further my theory of Geometric Unity suggests an inevitable universe that bootstraps itself into emergent existence from nothin
2018
1/ "Theories of Everything": A Taxonomy.
It is often said that "Theories-of-Everything are a dime a dozen" or that "All theoretical physicists worth their salt have several in a drawer." So far as I can tell, this is simply untrue. We've barely ever, if at all, seen candidates.
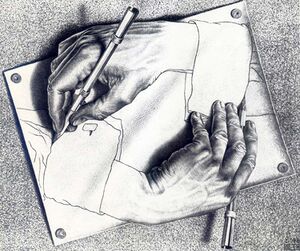
2/ The Escher Lithograph used in the first tweet points to the core of why TOEs are rare. A candidate TOE has to have some quality of "a fire that lights itself", which is difficult to think about beyond the equations that would instantiate it. Hence very few such theories exist.
3/ I'm going to lean on the following dictionary of analogies:
Physical Paper = Void Pictured Canvas = Manifold and/or Einsteinian Spacetime Ink=Matter & non-gravitational force fields Pencils = Pre-Conscious Lego (e.g. amino acids) Hands = Consciousness Paradox = Self-awareness
4/ In my taxonomy, Type I TOEs are our least ambitious but they best match our state of the world. They are distinguished by two *separate* sources of origin: one for the Canvas (General Relativity or Witten's point i) ) & one for the Ink (Standard Model or Witten's point ii) ).

5 Type II TOE's are more ambitious & seek to derive the Ink from the choice of a mathematically distinguished Canvas that is anything but blank. My arch-nemesis @garrettlisi's theory is Type II. E8 is his 248 dimensional canvas. The intricacy is there, but doesn't quite match up.

6/ In Type III TOEs the ink is to be derived from canvas, but the canvas is essentially blank; it simply permits mathematics to happen (e.g. calculus and linear algebra). In such theories the ink has to be bootstrapped into existence. My lectures on Geometric Unity were Type III.

7/ Type IV TOE's try to change the question from Einstein's "Unified Field Theory." In String Thy, "Quantizing Gravity" became substituted for "Unified Field." For this crowd, many are now betting that the canvas & ink are both *emergent* from some deeper fundamental quantum thy.

8/ Type V TOEs are of a type I've never been able to fully contemplate; they are without boundaries or origins. There is no "Why is there something rather than nothing" within them. That which is not forbidden is compelled into existence. Void creates canvas & canvas begets void.
9/ Type VI TOEs begin with the hands. Religions are of this type. I pass over this in silence as they aren't scientific.
I will leave open higher types, but I've really only seen attempts at I-IV & I wouldn't call String-Thy/M-Thy a full TOE try since events of the last 15 yrs.
10/ I believe fundamental physics is stalled out because we are finally at the doorstep of a TOE and we haven't really bothered to think about what that would actually mean because we've never been here before. A final step need not look like any previous one. In fact, it cannot.
END/ My bet is on Type III for a reason:
Type I is not unified.
Type II is possible, but appears to be unworkable in details.
Type IV appears to lack sufficient guidance from Quantum theory to actually 'ship' despite consuming resources for yrs.
Types V & VI lack any progress.
1/ APRIL FOOLS' SCIENCE: Theory into Practice.
I was challenged by someone as to why I wasn't taking my own medicine referenced in the sub-tweet below this April 1st. Ok. Here goes.
What I believe about the universe that is quite different and why I don't talk about it much...
1/ APRIL FOOL'S SCIENCE: A proposal.
Already bored of the coming "April Fools' Day!" pranks? Same here. And it's still March!
Consider how we might re-purpose this resource for science. What if 1 day a year, we explored big ideas that'd normally result in professional shunning?
2/ When I was around 16-17, I learned of a story that fascinated me much more than it seemed to captivate any other mathematician or physicist. It was the story of the discovery of the "Wu-Yang" dictionary around 1975-6, involving 3 super-minds: Jim Simons, CN Yang & Is Singer.
3/ What was learned was that the Quantum of Planck, Bohr & Dirac was built on an internal Geometry, just as surely as General Relativity was built on an external geometry of space-time. Only the two geometries weren't the same! One was due to B Riemann; the other to C Ehresmann.
4/ Further the 2 geometries had different advantages. Riemann's geometry allowed you to compress the curvature & measure the 'torsion' while Ehresmann's encouraged "Gauge Rotation"... as long as you didn't do either of those two things. So I asked could the geometries be unified?
5/ This would be a change in physics' main question. Instead of asking if Einstein's gravity could fit within Bohr's quantum, we could ask "Could Einstein's structures peculiar to Riemann's geometry be unified & rotated within Ehresmann's?" The answer was almost a 'No!'
Almost.
6/ While physicists said the Universe was known to be chiral, I came to believe it was fundamentally symmetric. While we seemed to observe there being 3 or more generations of matter, I came to believe that there were but 2 true generations, plus an improbable "imposter." etc...
7/ In short a great many things had to be slightly off in our picture of the world in the 1980s to get the two geometric theories into a "Geometric Unity." Then in 1998, it was found that neutrinos weren't massless! This started to tip the scales towards the alterations I needed.
8/ In short the April 1st "trick" that is being played on me is that I see a *natural* theory where chirality would be emergent (not fundamental), the number of true generations would be 2 not 3, there would be 2^4 and not 15 Fermions in a generation, and the geometries unify.
9/ I spoke on this nearly 5 years ago; I have been slow to get back to it as I found the physics response bewildering. I have now decided to return to this work & to disposition it. So over the coming year, I'll begin pushing out "Geometric Unity" (as a non-physicist) to experts.

END/ I am sorry that this was a bit technical for lay folks and not technical enough for experts, but it's twitter. I may begin to say more in the weeks and months ahead that may be clarifying.
If you are interested, do stay tuned. Until then, I thank you for your time.
2021
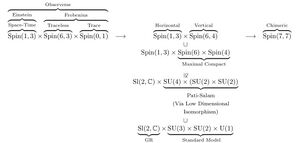
In strong GU:
SU(3) x SU(2) x U(1) (Standard Model)
Is contained in U(3)xU(2) inside
Spin(6)xSpin(4) =SU(4)xSU(2)xSU(2)
(Before the more difficult non compact Spin(6,4).)
I’d look first to the extra 1D reductive U(1) if the experiments hold up. Then to Spin(6) x Spin(4):
@EricRWeinstein What are your thoughts on this and how does it fit with Geometric Unity? https://www.bbc.com/news/56643677
As far as Fermion quantum number predictions that could open up new channels, Strong GU makes clear predictions. Explicitly, here would be the next Spin-1/2 particles internal symmetries we should find:
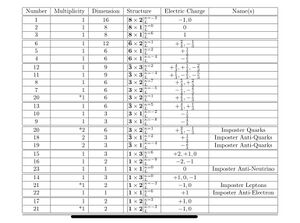
Additionally, Strong GU predicts that there will be 16 Spin-3/2 particles with Standard model symmetries conjugate to the Spin-1/2 generations and gives their ‘internal’ quantum numbers as:
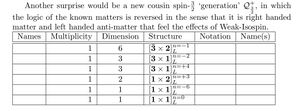
Now, why if GU makes predictions do I appear to some to shy away from them?
A: I don’t.
But string theorists hide the fact that they disconnected themselves from normal science by trying to force everyone else *except* String Theorists into answering hyperspecific challenges.
Thus while I can tell you what GU predicts is next, they push for a QFT calculation of energy scale to make others sound vague.
So let’s talk vague: Look at the above containments and SM quantum numbers. That’s not vague. Now ask String Theorists the SAME question...and compare.
Lastly: I would caution about getting too far ahead of our experimentalist friends. Let them sort out their confidence and not push them to be too definite prematurely.
But my advice is to watch *relative* predictive responses of those w/ “Beyond the Standard Model” theories. 🙏
P.S. Happy to attempt to sharpen what GU can say. But not working on my own outside the community. If you want more precise predictions than I already have, I’d need access to normal resources (e.g. constructive QFT colleagues). Working outside from home it’s probably impossible.
P.P.S. Remember that GU rejects three generations. In GU it’s 2 True generations plus 1 imposter. A priori, this could also be an effect of the imposter not being a true generation.
Again I would need QFT colleagues trying to help me see if that is a possible effect.
Let’s try this again. This has almost no engagement. I’m not buying it Twitter.
We are on our way to having physics declared beyond the Standard Model with new matter/force needed. And, this is quite specific as to what Geometric Unity says comes next: https://geometricunity.org
In strong GU:
SU(3) x SU(2) x U(1) (Standard Model)
Is contained in U(3)xU(2) inside
Spin(6)xSpin(4) =SU(4)xSU(2)xSU(2)
(Before the more difficult non compact Spin(6,4).)
I’d look first to the extra 1D reductive U(1) if the experiments hold up. Then to Spin(6) x Spin(4):

Please retweet the quote tweeted thread above to get sound the Twitter algos. 🙏
Unlike many theories, GU can already predict a lot about what comes next and even tells us that we have things wrong about particles we think we already know and understand: Why the Muon g-2 Results Are So Exciting!

Pentagon confirms leaked photos and video of UFOs are legitimate https://www.theguardian.com/us-news/2021/apr/16/pentagon-ufos-leaked-photos-uap
I do wish people would understand that GU is rather serious and what it is attempting to say with new particle predictions, geometric possibilities and additional *temporal* dimensions.
Even if you assume it is wrong, it is the only attempt of its kind of which I am aware.
At this point, the story I am tracking isn’t “Little Green Men”. It is “Officials inexplicably change course on UFO narrative”.
Also, the story about “Technology never before seen.” Would make more sense with “Technology” replaced by “Physics”.
High level government officials have given UAPs credibility, but it's still pretty hard for an outsider to analyze the evidence objectively. It's all video footage and testimony. We need much stronger evidence to form any real opinion on UFOs being extraterrestrial or not.
The US/Europe seriously diverted attention from doing real theoretical physics almost 40 years ago in 1984 to explore physics inspired mathematics. Did China/Iran/Russia/Israel? I don’t know.
But I can tell you this: no one in government is appropriately focused on new physics.
Imagine in 1900 some “crank” told you about thermonuclear weapons. Would you listen or laugh? Well, they’d be only 5 decades away with no aliens necessary. And powered flight hadn’t happened yet!
That’s how powerful a “new physics” advantage is. We’re behaving like lunatics.
Any time ANYONE at least 1/2-way viable says something weird or kooky or interesting (Wolfram, Lisi, etc.) the cost of a Department of Energy 1hr phone call is negligible. Almost no one with that background says anything like this. Maybe less than 1 such PhD “lunatic” per year.
Do I think Wolfram, Lisi, Kaku, Smolin, Klee Irwin, Sarfatti, Woit/Penrose etc are right or on the doorstep of new physics? No! But It’s also totally irrelevant to the security risk.
It wouldn’t matter to me at all. I would check in with all of them: the cost is zero. The risk?
The thing I like least about Geometric Unity is not being able to know what it would unlock if true, any more than Einstein and Bohr understood Lise Meitner, Stan Ulam & Edward Teller’s weaponization of New Physics.
We are talking about UFOs while not worrying about New Physics.
Think about the g-2 muon anomaly. Have you heard as much about that suggesting the possibility of New Physics from high precision (rather than high energy) as you have about the TicTac UAP?
Similarly, how often do you hear about UAP technology rather than physics issues. Right??
I have no idea what to make of the change in the UAP narrative. What I can tell you with certainty is that for such an ENORMOUS change in the narrative there is no sane explanation for the DOE not to be talking new physics risks and taking every one of the few claims seriously.
As we saw over & over in the 20th century, any small change in physics can change everything almost overnight. From A-Bombs to Semiconductors.
The handful of PhD level claims are of negligible cost to investigate & dismiss compared to a single fighter jet.
DOE lost the plot.
Enough! Let’s get back to UFOs and space opera so we don’t have to worry about China & Iran making a breakthrough on a white board in some lab we can’t see.
Moral: if you take UFOs seriously but not the risk of new physics, you aren’t thinking clearly.
Just think about it. 🙏

I may be confused, but I see a world dissolving in a rainbow of spectral Nihilism: anti-natalism, critical theory, post-modernism, equality of outcome, etc.
Great music doesn’t save the world directly. It viscerally reminds us of why humanity is worth saving. GU may fix this.
Lol while his brother is trying to save the world erics...
While @sapinker points out how many things got better, he doesn’t address the elephant in the room: The Twin Nuclei Problem.
@BretWeinstein focused on one nucleus. I’m focused on the other. Almost everyone else is focused on *neither*.
So listen to some music & pick a nucleus.
Lastly, song, film, letters, poetry, wealth, luxury, aesthetics, pleasure, delicacies, laughter, eroticism, dance, etc often take on their greatest significance in times of war & peril by sustaining us past the point of mental exhaustion & defeatism. Expect MORE from the above.🙏
Dear @michaelshermer,
Thanks for this. Very sober. I myself also don’t find the authenticated videos so far released compelling. But I do find your challenge of “no isolated discontinuous innovation” quite interesting!
Might I propose a friendly debate among friendly skeptics?
Dear @EricRWeinstein Please see my argument for why UAPs cannot be foreign assets capable of physics & aerodynamics attributed to UAPs that if true would be decades or centuries ahead of us. History shows no nations/companies of comp development so lag. https://quillette.com/2021/06/03/understanding-the-unidentified/
First of all, I am concerned that the paradigm of being scientifically or technologically “centuries ahead” is all wrong. This came up in a phone call with our buddy @SamHarrisOrg.
Q: How many centuries ahead is 1952-3 from 1900? I’d have guessed “many” (not .5) and been wrong.


Next challenge: doesn’t your line of reasoning prove that “Renaissance Technologies” is either a fraud or a front? Their Medallion Fund is otherwise a long term unbreached secret, discontinuous from any other know investment fund seemingly thousands of years ahead of competitors.
Now I’ve had the odd question about Renaissance (front not fraud) for just this reason. But either way, it’s either a counter example to your claims on discontinuous innovation if it is merely a fund or a counter-example to your secrecy claims if it is our secret physics program.
Next: there are really two metrics on innovations.
Metric I: How big the incremental jump in difficulty.
Metric II: How big the jump in what is unlocked.
The great fear is that a small jump measured by 1 leading to an ENORMOUS jump in as measured by II.
You are, to me, arguing powerfully that certain people can’t exist: Rodney Mullen, Edward Van Halen, Bob Beamon, Dick Fosbury, Hiroji Satoh, Satoshi Nakamoto, etc.
They all exhibited the “a little unlocks a lot” paradigm with Zero-Day exploits that were each decisive.
And that brings us to theoretical physics. Beginning around 1982 , the son of the world’s top employed anti-gravity researcher(?!) of the 1950s turned in what may be the most impressive 15yr output in the history of the subject by my estimation. How can I begin to explain this?
It’s not physics exactly. But Edward Witten w support from a small number of folks rewrote Quantum Field Theory as geometry. If Einstein geometrized gravity, then Witten geometrized Quantum Field theory (everything else).
Now, all that change has so far unlocked exactly nothing.
But it’s not that nothing happened in physics. While we were pretending that string theory was working, Witten & Co revolutionized our mathematical framework. Think of it as an enormous amount of unrealized gains. Pent up genius & power looking for its 1st application to the 🌎.
If you gave us E Witten, J Simons, I Singer, CN Yang, M Atiyah, D Quillen & G Segal, in a quiet program in 1975, I could argue that they didn’t need much more. In fact you don’t need all 7 but for the sake of argument I can make the case using this. But Witten is the main engine.
Now let me show you how I could get discontinuous innovation if I were China or Russia. I don’t know those systems as well so I’ll use the US example.
We know most of the top minds. We pretend that there is a lot of subjectivity about this for social reasons but China wouldn’t.
If I thought like CCP, I’d create a lavish secret theoretical physics program modeled on the Russian Sharashka system. The key would be to get it to look like something else. A boring Tech company or some weird Chinese fund to disguise the reason for the secretive lavish campus.
[Digression: If the US were smarter, we’d do it by setting up a mythic secret $B hedge fund that employs top differential geometers, theoretical physicists & ML experts by a national lab & an off brand university w/ inexplicably strong geometry & physics. But enough crazy talk..]
If CCP could today repeat what Witten (& friends) did building off Geometric Quantum Field Thy, the US would have Zero clue what it unlocks. Even by your own incrementalist theory. It might unlock absolutely nothing. Or passage to the stars via additional degrees of freedom. 🤷♂️
One last point. I released such a theory. Could well be wrong.
But I can tell you I should have received a call from DOE. Because calls are cheap and relevant trained PhDs are *very* finite. The US should track every geometer, General Relativist, and Particle Theorist working.
You don’t have to take a position on me or GU. You can ask Wolfram or Lisi or Barbour or Deutsche or anyone outside the system whether such calls are placed. They are not. No one *in* the system believes in wild discontinuous change from *outside* the system. As per your article.
Which is to say we’re not monitoring. Maybe we think that’s a waste of taxpayer dollars. Maybe we think that a Grisha Perelman of physics is impossible.
How much does a phone call cost if a researcher is wrong vs not bothering if they’re right? Price the Type I & II error. Nuts.
Discontinuous innovation is always unlikely. But never impossible.
We are both skeptics. But this UFO story is weird beyond belief Michael. I can’t think of a single story to fit to these reports I’m hearing about.
I welcome your thoughts. As always.
Warm regards,
Eric
France just opened up and I’m honored to have been invited to give the first in person GU presentation post COVID at Centre de Physique Théorique in Marseille. It’s on 6/22 at 8am ET/5am PT.
Join Zoom Meeting
https://univ-amu-fr.zoom.us/j/95582769808?pwd=TkZRaFJpdjZEUXVySlV1K3hKMTlhQT09#success
Meeting ID: 955 8276 9808
Passcode: 674264
I have two bits of information about JE that are not public.
1) An interchange from McAfee on Epstein.
2) Knowledge that Epstein was asking after me in a late email just before he died. I have no idea why. There is no more contact about Epstein than one meeting about 20yrs ago.

I’m quite concerned now given John’s 2020 call.
I subscribe to an unpopular position. Consider 3 kinds of 🌎:
A) Ones with no life or at least no life within striking distance of the source code (ToE).
B) Worlds that are on the verge of gaining the source code but are confined to a terrestrial surface.
C) Root level access.
I see your point, but I would ask, wouldn’t there be a difference between basic recognition and categorization, and actively studying and interacting? One would assume that other species would still be resource and time limited, therefore forced to prioritize their attention?
Now, if you can jack into the cosmos as ‘Root’ it MAY facilitate stuff that’s unimaginable (e.g. dimension hacking) yet only one remaining big upgrade away from being able to fuse nuclei. Which is where we are now.
I’d guess all civilizations that are Root care about each other.
The following is pure speculation (Tutored by experience w/ GU):
I think we sent a signal to the cosmos in 1945 and then on Nov. 1, 1952. Fusing Nuclei is what you do JUST before you become root. If this is right, we let the cosmos know “Earth is root adjacent” w/o awareness.
Is there anyone in the cosmos listening? Perhaps not. But we are all acting as if living on a terrestrial surface with the ability to fuse nuclei is some totally normal thing due to <70 years of good luck. Which is insane.
Now what if I’m right in the above and the cosmos cares?
The idea of a newly space-time-faring unwise civilization with fresh root level access is a nightmare. And no one but no one on earth takes this seriously anymore. After 1952 fundamental physics went on progressing normally for ~20yrs. So after that it’s been~50yrs of stagnation.
In those ~50yrs we learned to stop worrying. About Fusion-weapons, interstellar travel, a cosmos that listens or even our ability to progress to the end. In 1984, physicists were talking about the end of physics without irony. They then failed, while failing to report failure.
So they told another story: “String theory didn’t fail!! It may take 100s of years to figure it out!” That is “If we String Theorists can’t make progress, a Theory of Everything is now far over the Horizon for everyone else.” But that’s not logically necessary. I say we’re close.
It makes sense to worry about *every* small boutique program: Lisi, Wolfram, Barbour, LQG, Tegmark, ConnesLott, Octonions, amplitudhedron, etc. Our science/defense establishment doesn’t seem to get this idea: after 50yrs of no progress it seems too abstract to practical men.
I learned from my buddy @SamHarrisOrg that he thought 👽 would be Millenia ahead of us. Look at Nov 1, 1952 from Nov 1 1902: you don’t have powered flight, know what relativity or the quantum is, know that neutrons exist, know about anti-matter, etc.
From ‘02, ‘52 IS millennia.


Well, we may or may not have a major update in our future. And if it unlocks dimension hacking, looking glass matter, VEV/potential hacking, multi-temporal pseudo-Riemannian metrics, Dark Chemisty, Dark Light, additional families, RaritaSchwinger fields, etc then we get upgraded.
And I believe all at once.
What does that mean? I honestly don’t know.
But Imagine you sent a chainsaw, a Bugatti, Ibogaine, “My-1st-Crisper”, and an F-18 to a badly behaved 5yr old child for a birthday present w a simple card: “Enjoy!” We’d worry specifically b/c immaturity.
That’s what NDT has most wrong. He thinks we are far behind anything that could visit us, but that ISN’T backed up by science. He’d have to explain why we aren’t “root adjacent” right now or that root buys us nothing. Well?
Think of the relationship of Iran to nukes for example.
Iran is now Nuke adjacent. And their facilities and scientists keep running into mysterious problems. Why? Surely not because Iran is too insignificant to her more advanced neighbors. That would mirror NDT’s argument. My argument is that root level access to nuclei *suffices*.
Am I saying “Aliens are here”? Of course not. But the “Root Adjacency Hypothesis” is not properly discussed almost anywhere. Which defies all explanation.
Perhaps everyone else is right & I’m wrong. Absolutely! But it’s common for the world to make a crazy dumb idea a consensus.
And I think NDT is enforcing a dangerous “Copernican” consensus that we are too insignificant to even monitor or visit, to go along with “We’ve had Nukes for 70 years without losing a city. I wouldn’t worry. What could possibly go wrong.”
This is just a human rationality flaw.🙏
I don’t believe in FTL travel.
FTL is an implicit appeal to travel *within* Relativity theory. Presumably traversing the spacetime manifold of Einstein faster than his theory allows.
The goal is to ask what theory is *beyond* Einstein & might it allow us the *illusion* of FTL.
Can you describe faster than light travel in practical layman's terms?
An example: In GU, relativity theory is recovered from the Observerse which is constructed around two separate spaces X and Y. Einstein’s Spacetime (a signature (1,3) 4-manifold with pseudo Riemannian metric) is recovered from observations of Y by X.
Another example. Some see spacetime as the commutative limit of a non-commutative manifold. That would be beyond relativity.
Others see topology changing operators that allow agents to change spacetime topologically. Again that would be beyond the usual relativity theory.
But in standard Relativity theory as an effective theory, I don’t think about FTL. Sorry.
My friend & work colleague, Jesse Michels over at @AlchemyAmerican, is starting his podcast/video series.
As the original producer of ThePortal, he interviews me here about its start, GU, etc.:
Give him a subscription and let’s see where he takes this.
Wanted to thank the High-Energy theory group in the physics department at @uchicago for the invite to visit & speak on GU in the Kadanoff center. Thanks in particular to my colleague Savdeep Sethi for a lovely visit over a couple of days.
Great Folks + Chalk + Slate = Happiness.




Wow. I’ve never once seen these quotes.
And what have I been warning about? Either 4 or 6 extra temporal dimensions. Same deal.
No more arrow of time. Time would become a higher dimensional whirlpool. But this is a fringe area of respectable physics. Not crazy enough to ignore.
Is there anything to this? Don’t know. I spoke to Hal Puthoff about it. Didn’t get much of a reaction. But secrecy is secrecy. And I respect that given what would be at stake.
But strong GU predicts 7 or 5 total *temporal* dimensions as the most likely total number. A big shift.
Still, it is striking to hear this is being discussed by Elizondo and others.
2022
Looking forward to talking to my colleague and friend, the noted skeptic @michaelshermer in less than an hour at https://t.co/2a2I4gP5cd as part of @HTLGIFestival to discuss the Multiverse and the GU Observerse.
Join us!
At 12:30pm ET/9:30am PT today I'm in conversation with @EricRWeinstein about his Geometric Unity theory of everything at the big UK @HTLGIFestival Lots of interesting talks on consciousness too. Join us if you are of a mind: https://howthelightgetsin.org/events/eric-weinstein-in-conversation-with-michael-shermer-6218
Under Newton, we were free to explore the cosmos: 1686-1905.
Einstein then enforced house arrest to our solar system:1905-Now.
@elonmusk then said chemical rockets could get us 2 more spheres w Newtonian laws.
But survival hinges on going *beyond* Einstein, not back to Newton.
Did you really say that, Eric?
Like EVERY civilisation before us, not destroyed by some rival, we are on course to self-destruct long before we become a multi-planetary species.
Your Brother, Bret's, #EvolutionaryLens should reveal this to him, but doesn't seem to have done.
I’m not going to complicate the basic story with caveats. That’s the basic plot.
Either there is freedom to leave based on new ideas, like GU, or the Einsteinian restrictions will persist.
If they persist; we probably can mildly elongate survival here by decades via wisdom.
But if we can leave to explore the universe by going beyond Einstein, anyone else out there can visit.
This brings us to UFO/UAP. Assuming a distribution of life in the cosmos:: some life is behind us in science, with others ahead.
A (loose) argument then links UAP to survival:
If life is abundant & we’re not the top of the hierarchy (which is reasonable to me), I’d guess that UAP would be here if that is possible in Einstein’s successor theories. The absence of UAP is strong but *inconclusive* proof that Einstein’s restrictions persist in all theory.
Hence my interest in UAP. UAP from distant worlds would be a strong indication that it is possible to diversify our shared risk which is that all known technological life is dependent on one atmosphere linking our three main existential risks:
A) Climate
B) Pathogen
C) Radiation
So if #ufotwitter ever wanted to know why I didn’t take #UFO seriously, it was because I thought it was *preposterous* given lack of evidence.
And if #ScienceTwitter wants to know why I spun on a dime, it’s because it IS linked to the post-Einsteinian physics of our survival. 🙏
1) General Relativity
2) (Pseudo-)Riemannian Geometry
3) Quantum Field Theory
4) Material Science/Condensed Matter
5) Nuclear Physics/Weaponry
6) Disinformation Theory
7) Cult Indoctrination/Deprogramming
8) Propaganda
9) Preference Falsification Theory
10) Mansfield Amendment
@LueElizondo recently gave a small list of topics he would recommend for study to begin to wrangle "the Phenomenon", if he "were king". What areas of intersectional learning do YOU think are needed and should be more deeply looked into? Your ufology curriculum. Thanks, Eric.
11) Science Policy Theory (V Bush)
12) Selection (Abstracted)
13) Comparative Eschatology
14) Anti-Gravity Pseudo-science involving top physicists and mathematicians in the era of the So-Called ‘Golden age of General Relativity’.
15) GU
16) Mind control.
Remember: you asked! ;-)
Willing to answer a few more Tweets on the San Marino UAP conference where I unexpectedly was asked to fill in for @LueElizondo. I’m likely to get throttled & harassed yet again. When and if the beloved Twitter nanny algorithm starts again, I’ll call it a night here in Rome.
Go!
Has any of this episode inspired you to pursue your GU theory with greater zest? Is there an interdimensional route opening?
There is a lot of loose talk about dimensionality. Keep in mind that I have zero direct evidence of the phenomena. So this is wildly premature.
My interest here is that GU replaces one manifold with two in a bundle structure and adds BOTH temporal and spatial dimensions.
As the author of GU, I still don’t know how to think in multiple temporal dimensions. The math is quite exotic. But I at least know through GU that the math can FORCE us to confront ultra hyperbolic PDE. It would change everything we know if unscreened. No simple Hamiltonian.
I wish people would stop talking about higher dimensional beings though. If GU is on point, then we are also higher dimensional beings. So I could do without Exoticism. If this is in any way real, we should reserve speech for precise meanings. And I don’t know if it is real. Yet.
Astrophysicists make observations consistent with the predictions of an alternative theory of gravity https://phys.org/news/2022-10-astrophysicists-alternative-theory-gravity.html
@EricRWeinstein come teach.
Let’s go slow. GU has GR as a sub theory. So if GR was wildly wrong, it wouldn’t be good for GU. It pays to be excited with extreme caution. I hadn’t seen this though. So thanks!
So,I was ̶d̶e̶r̶a̶n̶g̶e̶d̶,̶ ̶d̶e̶l̶u̶d̶e̶d̶,̶ ̶u̶n̶h̶i̶n̶g̶e̶d̶,̶ ̶p̶a̶r̶a̶n̶o̶i̶d̶,̶ ̶s̶t̶u̶p̶i̶d̶,̶ ̶u̶n̶i̶n̶t̶e̶n̶t̶i̶o̶n̶a̶l̶l̶y̶ ̶h̶i̶l̶a̶r̶i̶o̶u̶s̶,̶ ̶c̶r̶i̶n̶g̶e̶,̶ ̶p̶a̶t̶h̶e̶t̶i̶c̶,̶ ̶g̶r̶a̶n̶d̶s̶t̶a̶n̶d̶i̶n̶g̶,̶ ̶a̶ ̶c̶h̶a̶r̶l̶a̶t̶a̶n̶,̶ ̶n̶u̶t̶t̶y̶,̶ right all along?
8. Federal intelligence and law enforcement reach into Twitter included the Department of Homeland Security, which partnered with security contractors and think tanks to pressure Twitter to moderate content.
Word to the wise: watch when they figure out the work on CPI and, most importantly, GU. “Gonna be lit.”
Same story, but on steroids: institutions can’t deny reality at this scale forever. Too many enormous lies to maintain indefinitely . The instit. Kayfabe collapse is coming.
2023
I want to use the argument made to make a point. “Light years” is a mathematical concept. Newtonian gravitation & Einstein’s general relativity are our past & current mathematical maps of the physical “territory”.
The Map ≠ The Territory.
I’m focused on post-Einsteinian maps.
You know the laws of physics, you understand probability, you understand how many stars are within a 100 light years of Earth. ... So let us stop pretending there is any possibility that this is nothing more than a con.
I don’t know how to answer. I believe that the world beyond Einstein does not have a 1,3 metric where that 1 means a single future.
If I’m correct, the world is 7,7 or 5,9 pulled back to 1,3. So I decline to answer: I don’t know how to think about my own model’s pasts/futures. https://x.com/cdse2403/status/1638538814086889472
As I have said in public, I find it EXTREMELY difficult to conceptualize multiple temporal dimensions. Just because I can see that they are there in my model, does not mean I am smart enough to understand their consequences. Sorry to disappoint. Try Itzhak Bars at USC?
Be well.
Perhaps one simple thing I might add is that only with one temporal dimension do boundary conditions become initial conditions. Boundary conditions are more general and Ultra Hyperbolic equations can be defined so that Hyperbolic relativistic equations are a quirky special case.
I don’t know how to answer. I believe that the world beyond Einstein does not have a 1,3 metric where that 1 means a single future.
If I’m correct, the world is 7,7 or 5,9 pulled back to 1,3. So I decline to answer: I don’t know how to think about my own model’s pasts/futures. https://x.com/cdse2403/status/1638538814086889472
If gimel is native to X, then what is the pullback of gimel? Or is gimel native to Y?
Gimel pulls back field content native to Y back to X. Gimel^{1,3} does the pulling back of the data (sections over Y). It is the stylus that samples the record Y^{7,7} (or Y^{5,9} in the second GU variant that is physical) and plays it back. In GU, spacetime is just the Victrola.
Now I feel completely alone.
I want our wanting out of this story. I have a huge dog in this fight. I spend every day fighting my own human desire for GU to be proven correct.
I believe this is how String Theorists stopped being scientists.
I just want our data & the physics.
If biological aliens were here from others star systems in crafts that defy the current physics of the standard model and, more importantly, general relativity, I would be one of the few people who would have a guess on day one as to how they must have gotten here. It’s tempting.
I don’t think biological interstellar alien visitors using GR and the SM make much sense. So I try to have a war *inside* my own mind as to what is true. I have a genuine “Need to Know” as to whether this is BS NatSec space opera disinformation theater. Because to me, it is data.
What just happened isn’t data. It’s that a sober individual just pushed one of the many longstanding highly conserved NHI narratives collected from *many* diverse sober NatSec informants over the sworn testimony line. And it gets a LOT crazier from here. But it’s not science yet.
As I‘ve been saying, there is so much deliberate NatSec BS out here that our own scientists are being propagandized. We’re drilling holes in our own scientists’ lifeboat. Last time we saw this it was virologists/immunologists/epidemiologists being gaslit. Now it’s physicists.
Let me be very careful in what I am about to say. We have at least the appearance and optics of scientific self-sabotage. And wanting things to be true is how science dies.
I fight like hell to promote my theory. But I’d sign on to another to know the truth if I was wrong.
We may be looking at the birth of a new UFO religion. Or a moment of contact. Or a long running Disinformation campaign. Etc.
To go beyond GR, let’s be scientists & get NatSec out of our data first. Where is our data pruned of space opera disinformation and cultic religiosity?
What I want to know:
Why was the Mansfield Amendment passed?
Why did NSF fake a labor shortage in our MARKET economy destroying American STEM labor markets?
What stopped the Golden Age Of General Relativity?
Why was the SSC really cancelled?
StringTheory & STAGNATION: WTF?
What the hell was the 1957 Behnson funded UNC Chapel Hill conference actually about?
Why are we not stopping to QUESTION quantum gravity after 70 years of public *FAILURE* inspired by Babson-Behnson patronage of RIAS, the Institute of Field Physics and the precursor to Lockheed?
This is the 50th year of stagnation in the Standard Model Lagrangian. It is AS IF we are deliberately trying to forget how to do actual physics. Everyone who has succeeded in Particle Theory in standard terms is now over 70. This is insane. In 25 years there will be no one left.
Why are we not admitting that quantum gravity is killing physics and is the public respectable face of 1950s anti-gravity mania that lives on to murder all new theories in their cradle?
Quantum Gravity is fake and works to stop actual physics.
There. I said it. Now let’s talk.
If you want to know whether there are biological interstellar visitors here observing us, the short answer is “Almost *certainly* not if they are using our current stagnant non-progressing theories of physics.”
Let’s finally get serious about this whacky subject? Thanks. 🙏
2024
Twitter over compensates for the very real madness of the institutional world.
Despite being seen as contrarian, here are some mainstream Physics opinions that I hold, which Twitter somehow finds controversial:
I don’t think The Universe is “made of Consciousness.”
I don’t think Dark Energy is “Sus”.
I think Dark Matter is real.
I don’t think the Standard Model is ‘bogus’.
I don’t think “universities are over”.
I don’t think String Theory (for all its problems) or String Theorists are stupid.
Etc. ——
Twitter is kinda just nuts. No matter how extreme my opinions are by real world standards, Twitter is always more extreme. Perhaps it is because people hold things that they claim are “opinions”, but which would require more details and knowledge to elevate to that level. For example, I don’t think I have an opinion on reasons of political economy for recent changes in the credit rating of Macedonian municipal bonds. So it is always surprising to see so many accounts claiming to hold strong heterodox opinions on wormholes, dark matter or the Big Bang.
I will respond to a few responses here to give an idea of what is going on X/Twitter.
Tweet 1. In physics, equations often don’t balance. So we add terms to account for what we can’t YET directly detect. The Neutron, quarks, Higgs field and Neutrino all had such an origin. By now all have been directly observed and fairly well modeled.
This is why I point out that neutrinos are basically dark matter, but for the weak force as the only non gravitational force to couple to them and affect them.
Dark is a spooky and misleading name for these which makes dark energy and dark matter sound similar. They aren’t.
Think of dark matter as being “decoupled matter” and/or “ultra heavy matter we can’t see at current accelerator energies” and it might seem to be less suspicious.
I don’t yet have a comparable suggestion for dark energy. Sorry.
Dark mater and energy are concepts I just can't wrap my head around.
Tweet 2:
“Theory of everything” as an idea confuses people. It’s sorta a string theory branding problem. The store “Just Tires” also does oil changes.
String Theorists relentlessly used “Theory of Everything” to grab our attention just as a store that wanted a simple message. Surely a theory of everything would scientifically explain “Why is there something rather than nothing?” just as “Just Tires” would surely not do oil changes.
Well, both went bust but couldn’t change their branding.
Even if is ultimately accepted as a TOE, Geometric Unity *cannot* explain why there is something rather than nothing. TOE is a term of art meaning that the input is something natural and simple and the output is presumably complete as the rules for the universe.
A TOE is more properly an attempt at the answer to “Why do the rules for everything unpack from assumptions so simple as to defy further scientific interest?” GU attempts to unpack from the assumption of 4-degrees of freedom (a manifold) and a tiny amount of natural structure like orientations and spin structures that are geometric and natural. It doesn’t explain from where that came.
A TOE doesn’t seek to put the theologian and philosopher out of business.

If the initial condition of all reality was absolute nothing there would be nothing in nothing to bring about something.
Tweet 3:
Honestly, I don’t even know where this comes from. I’ve spent thousands of hours in physics departments and never heard this discussed seriously. Even Roger Penrose’s theory about the quantum mind isn’t taken at the level of his other work.
I think the best that can be said for this as a scientific theory is that Physicists are finally admitting that the collapse of the wave function isn’t totally clear on what an observer or observation is. So consciousness can try to sneak in here as the missing ingredient.
I think this is an artifact of language. If we called the observer the collapser and had admitted we didn’t know what we meant exactly rather than trying to Pretend we did, it wouldn’t invite this much attention.
We should just admit that the notion of “the observer” is both mysterious at a field theoretic level and badly named.
And for my two cents, I’m betting an observation is in part something called “Pull back from the total space of a bundle via a section”. This boring and dry language wouldn’t cause mostly lay people to seize on consciousness as a solution.
Okay. I’m out. Back to sleep. Appreciate the kind words and questions.
Thank you. 🙏
This one tweet has made dark matter so much more understandable than the last 20 years hearing about it. Thanks as always Eric.
I'm confused. This lecture doesn't negate the geometric foundations of GR. Einstein differentiates between how gravity and electromagnetism relate to the structure of space, all the while pointing to his ultimate goal of unification. As for the rest of the original article linked, I'm unsure how the quotes from Einstein support the author's title. GR is indeed a geometric theory; however, Einstein's viewpoint was that its geometric nature doesn't singularly distinguish it from the broader domain of physics, where geometry has always played a fundamental role. If anything, Einstein is saying not to confuse the map with the territory.
He is correctly anticipating the Simons-Yang discovery of the “Wu Yang dictionary”.
Maxwell became Yang Mills Yang Mills became Simons Yang. Simons Yang became the Wu Yang Dictionary. Wu Yang was (except for one entry) was Ehressmann fiber bundle geometry.
Think of metric geometry, fiber geometry and symplectic geometry as the geometry of symmetric metric 2-tensors, fiber bundle connections and anti-symmetric 2 tensors respectively.
[Note for Curt: This is the whole point of Geometric Unity. They are three geometries. Which are all one geometry, and that is only possible in the rarest of circumstances. Which we are in oddly.
Metric Geometry: General Relativity GR Fiber Geometry: Standard Model SM Symplectic Geometry: Hamiltonian Quantization of the SM. ]
2025
Geometric Unity predicted that there’s no cosmological constant by replacing the frought term w/ a natural geometric varying field, invariant under symmetries.
I’ve given several talks on this recently in different physics depts. This was filmed at one in the U.S. in April.

A Universe without a cosmological constant? @EricRWeinstein presents a technical lecture @UCSanDiego on the future of Einstein’s “Biggest Blunder” in light of Geometric Unity & DESI’s newest results.
Watch:
To define this term, Geometric Unity constructs an Inhomogeneous Gauge Group as the source for the terms in the difference, and then replaces the Einstein field equations, term by term, with a new equation on a space of fields, far better behaved than Einstein’s space of metrics.

You ask:
Q: “What makes GU’s extra dimensions more physically grounded? Is there an observational path that distinguishes them, or are we still relying on elegance over first principles?”
A: Because, unlike String Theory, GU introduces *zero* extra dimensions. None. All 14 dimensions come from data within Einstein’s 4 dimensions.
Every Einsteinian space-time X^4 is ALREADY a section of the bundle of possible metric tensors. That bundle Y^14(X^4) has dimension 14 within General Relativity. All those 14 dimensions are endogenous and not extra dimensions. The data is all within X^4.
Extra means non-endogenous. These are endogenous.
SUMMARY. GU introduces no extra dimension beyond those already found in General Relativity. All data is within X^4.
[GU also introduces FAR LESS data than is introduced within the standard model. I believe there is no other theory that introduced fewer initial assumptions or is even close to GU in this regard.]
Thanks for the question.
Eric,
I have a sincere and respectful question for you.
You’ve rightly criticized string theory for introducing unobservable extra dimensions and for prioritizing mathematical elegance over empirical necessity. But in Geometric Unity, you also introduce additional dimensions (fourteen in total) to house the fields and symmetries needed for unification. While I understand these dimensions serve a structural rather than vibrational purpose, I’m wondering how we justify them any more than string theory justifies its own.
What makes GU’s extra dimensions more physically grounded? Is there an observational path that distinguishes them, or are we still relying on elegance over first principles?
Why not begin instead with the most minimal assumption: what must exist for the universe to behave as it does? Repulsion dominates the cosmos. Time governs emergence. Must we construct fields to explain what spacetime may already be doing by default?
With all respect, I ask whether our best hope for progress lies not in building more elaborate systems, but in returning to the simplest foundational questions.
Jerry
@EricRWeinstein Caught your debate with Sean Carroll on Piers. Why do you think he was spouting off so much misinformation about GU? "There's no Lagrangian!" I'm looking at the paper right now. There's literally 3 pages worth of Lagrangians like wtf.
Shhh. Have you noticed that you are like close to the only one who caught that? Explain that!
He just made that up. And no one noticed or bothered to check. And it is ALWAYS like this and has been for 40 years. I have no explanation. It’s completely beyond my comprehension.
Perhaps he was "instructing" the physics community:
"Act as though there are no Lagrangians"

That’s just it. I keep saying that the community is pretending. But it is actually lying.
Pretending there is no crisis.
Pretending that I am not in and out of physics departments all the time.
Pretending GU makes no predictions. Like in section 11.3 on pages 52 and 53 for example.
And we can quietly be here discussing this while Sean says he has read the draft in front of over half a million people that GU doesn’t make any predictions within it. Confident that no one will actually speak out with page numbers and screen shots and say “You do realize you are lying? Either about having read the draft or about the explicit predictions within it.”
Imagine you send a paper for peer review and you get Sean Carroll as your anonymous reviewer. He says he read it and there is nothing of interest. No Lagrangians. No predictions.
It has been *exactly* like this for 40 years. No one can believe it until they experience it. It has no explanation.

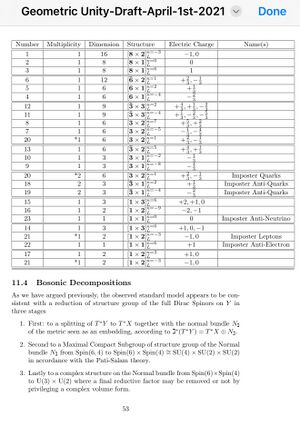
That's why your observation about peer review really being peer injunction makes so much sense.
Sorry Eric, I feel you, and I'm sure many more do too. The spell will break through, I believe that.
@codingquark @HeathHimself GU is both the most anti-interesting theory in history as well as the only theory that cannot be steelmanned.
@niederhaus17566 @HeathHimself If GU were right, that narrative would be wrong. And that narrative is the entire world to those who have devoted their lives to it for >40 years.
So GU must be madness. Which it is not.
@EricRWeinstein Caught your debate with Sean Carroll on Piers. Why do you think he was spouting off so much misinformation about GU? "There's no Lagrangian!" I'm looking at the paper right now. There's literally 3 pages worth of Lagrangians like wtf.
The whole debate was very odd, Carroll didn't offer a single criticism of any substance, not a single concept or equation. We need to remember Sean at heart is a philosophy and astronomy major, not a mathematician or physicist despite their self-styling
Not that you said anything wrong, but let me advance a different perspective. Sean’s work is a an undisclosed *direct* competitor to GU. Attached in a screenshot are the first three lines of his 1990 abstract.
Let me put them in the language of GU.
“The Chern-Simons Lagrangian has been studied previously in (2+1)-dimensional spacetime, where it is both gauge and Lorentz invariant. We the authors believe that outside of this special dimension, there is a fundamental trade off where we must either violate Ehresmannian Bundle Geometry (Gauge Theory of Particle Theory) or the pointwise Lorentz Invariance of Riemannian Geometry (Einstein’s General theory of Relativity). It appears to the authors that the right way to construct an analogous term in 3+1 dimensions is to create a Chern Simons-like term which couples the dual electromagnetic tensor to an artificial external four-vector which has no supporting evidence or motivation and violates both Einstein’s Special and General theories of Relativity. If we take this four-vector to be fixed, the term is gauge invariant but not Lorentz invariant throwing out one of the two pillars of modern physics. We do it anyway, because we believe the above mentioned tradeoff precludes any other approach.”
I personally knew Sean’s co-author Roman Jackiw decently well on this topic as he was at MIT. This was his perspective.
Why is Geometric Unity called Geometric Unity? Because we believe you can sacrifice neither geometry or the field will come to a standstill. It’s right there in the name. You need to have both Riemannian and Ehressmanian geometry to combine Gravity and Particle theory respectively.
Sean’s work is the DIRECT competitor of this GU theory. And GU sacrificed neither.

Given info on this link, why do you need Riemannian geometry in the first place if it is a subset of Ehressman?
https://chatgpt.com/share/68386b13-93e0-8013-a47d-75b2769f464d
Ah. It has two features that general Ehressmanian geometry generally lacks:
I) A distinguished Choice of Connection (The Levi Civita connection and the connections induced from it on associated bundles).
II) Tensor Decomposition coming from the lack of structure groups auxiliary to those of the tangent bundles.
So actually the specific sub geometry of (pseudo)-Riemannian geometry is an exchange of Gauge Symmetry and field content freedom for these two attributes.
Except in totally exotic cases. Like the one in which we oddly happen to live…but I digress.
@randallhump82 @soronoc @PiersUncensored @piersmorgan Interesting question right?
Well…consider that the dirty tricks effort to destroy GU appears to be run out of the world’s most powerful tech company using company assets. And it is where everyone stores their free email accounts…
Buckle up.
Was visiting Canada & dropped in on @TOEwithCurt Jaimungal. This is not the follow up to Curt’s 3hr GU documentary (?), but we hadn’t seen each other in some time & we decided to record. Hope you find it interesting.
We’ll try to do a proper sit down over GU at some point soon!
How crazy is theoretical physics?
Sidney Coleman was one of my favorite people in rheoretical physics. His office door was always open to me. And he was one of the only people who ever seemed to be “natively quantum”.
And he was hysterically funny.
I added a quote to a thread.

How it started: “anyone who knows this guy is a friend without an introduction”.
How’s it going:
I knew Sidney pretty well. I wasn’t a physicist or in his department, but I almost certainly knew him better than any other mathematics PhD student at Harvard.
Not enough to be a friend. But enough to call him a teacher and mentor. And a supporter.
He was somewhat scary, but suffered anyone gladly who truly wanted to learn.
He was super encouraging about GU but saw symmetry totally differently from my more geometric perspective so there was always a translation issue. He always wanted everything translated into Hilbert space symmetries rather than manifold symmetries.
One day he said something uncharacteristically “off” about the Large Exceptional Lie groups: F4 E6 E7 E8. It was uncomfortable because it was a sour note in the middle of an otherwise beautiful explanation. So I called attention to it.
He said something like “Do you know something I wish I knew here?” This was a first in our interactions. He clearly knew his perpective which succeeded everywhere else was not working as well here. Or really at all.
I explained my view was that we can’t properly intuit the large exceptional groups because they are all “missing” their linear defining representations. He asked “What Real dimensions?” I said that there were missing “phantom representation” modules in dimensions 24, 48, 96, 192. Respectively.
He said “What do you mean by that?” So I showed him their homogeneous spaces in dimensions 16, 32, 64, and 128. Respectively. Which clearly do exist.
He asked why if they are all projective spaces, that they couldn’t be deprojectivized. And I had to say “They all have classical anomalies. And ‘anomalies’ don’t always need to be canceled. Sometimes they need to be embraced.”
And he just smiled and said: “Right. Wow. Got it.”
————
Akshat: I don’t know you. But I thought you would enjoy who Sidney actually was. He was kind, mischievous, brilliant, generous and open.
Be well. And good luck.
Dear Dr. Weinstein, thanks for sharing this anecdote! It's very interesting, a wonderful share indeed. I misunderstood the context of the quote that you replied with (given the amount of trolling that happens on a daily basis on here). Besides that, nothing personal! :)
No worries. That was why I didn’t respond meanly. I was just mystified.
Sidney was irreverent and someone you would not want to cross…but he was also kind to fools whose hearts were in the science. Myself included. Just a gem of a mind and a mentor.
Related Pages
- Anti-Interesting
- General Relativity
- Geometric Unity Predictions
- I’ve Got a Good Feeling About This
- Peer Injunction
- Peer Review
- Quantum Gravity
- Quantum Field Theory
- Scientific Method
- Standard Model
- String Theory
- The Scientific Method is the Radio Edit of Great Science
- Why GU is a “Work of Entertainment”
- You Know You’re in GU When