Holonomy Project: Difference between revisions
(Created page with "== Title == Holonomy Project == Project Manager == ??? == Team Members == ??? == Prod URL == ??? == Dev URL == ??? == GitHub URL == ??? == Google Doc URL == ??? == Desc...") |
No edit summary |
||
| (47 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
== | {{InfoboxProject | ||
|project=Holonomy Project | |||
|image=[[File:Holonomy.png]] | |||
|topic=[[Graph, Wall, Tome]] | |||
|leader=EricRWeinstein#6876 | |||
|startdate= | |||
|customlabel1= | |||
|customdata1= | |||
|customlabel2= | |||
|customdata2= | |||
|customlabel3= | |||
|customdata3= | |||
|customlabel4= | |||
|customdata4= | |||
|link1title= | |||
|link1= | |||
|link2title= | |||
|link2= | |||
|link3title= | |||
|link3= | |||
|link4title= | |||
|link4= | |||
}} | |||
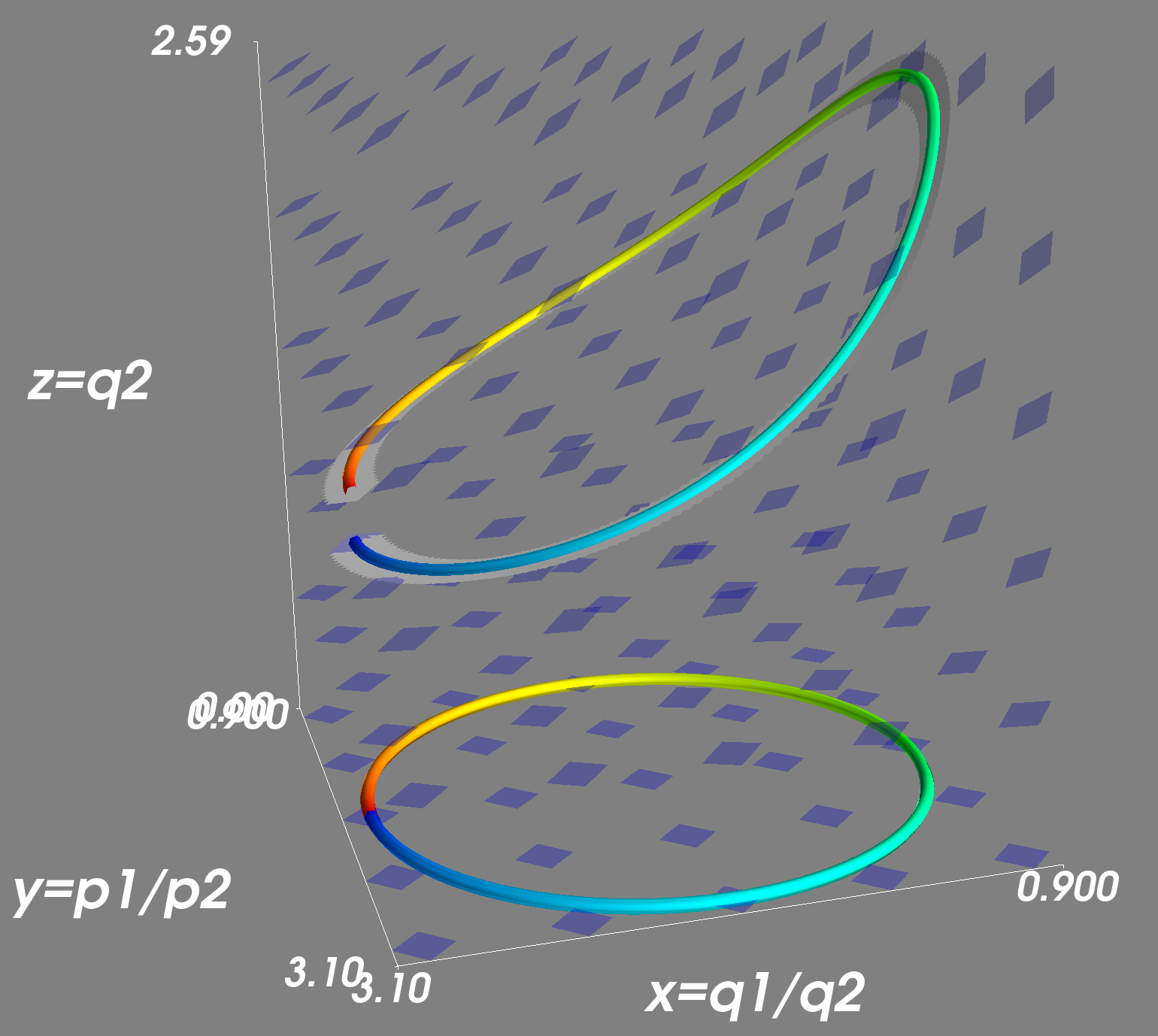
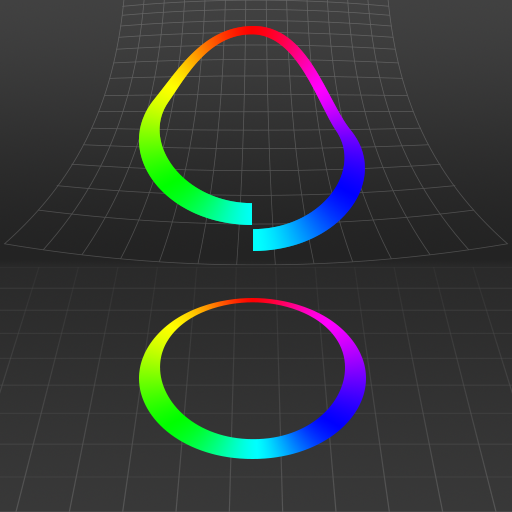
A visualization of the effect known as "holonomy", whereby parallel transporting a vector around a loop in a curved space leads to the vector changing upon returning to the start of the loop. How/how much the vector changes orientation/position in space is the holonomy of that loop in that space. This effect reveals deep information about the [https://en.wikipedia.org/wiki/Curvature curvature] of the space itself. | |||
= | <span class="highlight">Wait for Further News from Eric</span> | ||
== | == Goals == | ||
* Visualize holonomy to develop public intuition of the concept. | |||
== | == Demo == | ||
= | {{#widget:YouTube|id=fmDWCQs1bGI}} | ||
= | <div class="max-width"> | ||
https://theportal.wiki/images/7/7b/Holonomy_Example_-1.png | |||
</div> | |||
__NOTOC__ | |||
[[Category:Archive]] | |||
[[Category:Stalled]] | |||
[[Category: | |||
[[Category:Projects]] | [[Category:Projects]] | ||
[[Category:Graph, Wall, Tome]] | |||
Latest revision as of 19:00, 6 April 2024
| Holonomy Project | |
| |
| Information | |
|---|---|
| Topic | Graph, Wall, Tome |
| Leader | EricRWeinstein#6876 |
| Links | |
| All Projects | |
A visualization of the effect known as "holonomy", whereby parallel transporting a vector around a loop in a curved space leads to the vector changing upon returning to the start of the loop. How/how much the vector changes orientation/position in space is the holonomy of that loop in that space. This effect reveals deep information about the curvature of the space itself.
Wait for Further News from Eric
Goals[edit]
- Visualize holonomy to develop public intuition of the concept.
Demo[edit]