Graph, Wall, Tome: Difference between revisions
| (39 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
<div style="float:right;padding:20px;">__TOC__</div> | |||
Fundamental physics is an unknown world to most people. Equations, symbols, and incomprehensible terms abound, and unless you've studied post-grad mathematics and physics, this world is inaccessible to you. Although there are several great resources to map the way toward complete understanding. Most people will not undertake the journey to understand the source code to the world that we all inhabit. | Fundamental physics is an unknown world to most people. Equations, symbols, and incomprehensible terms abound, and unless you've studied post-grad mathematics and physics, this world is inaccessible to you. Although there are several great resources to map the way toward complete understanding. Most people will not undertake the journey to understand the source code to the world that we all inhabit. | ||
The goal of the Graph, Wall, Tome project is to solve this problem by building a portal anyone can use to travel to the amazing world that we call fundamental physics. | ''The goal of the Graph, Wall, Tome project is to solve this problem by building a portal anyone can use to travel to the amazing world that we call fundamental physics.'' | ||
The name of the project stems from the | The name of the project stems from the observation that there are three resources that themselves contain all that you need for an almost complete understanding of the world. | ||
# | # [[#The Graph|The Graph]] - A paragraph written by Edward Witten | ||
# | # [[#The Wall|The Wall]] - The iconic wall of Stony Brook University | ||
# | # [[#The Tome|The Tome]] - The book 'The Road to Reality' by Roger Penrose | ||
These resources are available to everyone, but will be sought by almost none. A goal of the Graph, Wall, Tome project is to convert these resources into a medium that can be widely disseminated, and which can not be ignored. | These resources are available to everyone, but will be sought by almost none. A goal of the Graph, Wall, Tome project is to convert these resources into a medium that can be widely disseminated, and which can not be ignored. | ||
| Line 21: | Line 23: | ||
Success will generate yet further insights, opening up a more fundamental understanding of the nature of reality - for the individuals involved, and - for humanity as a whole. | Success will generate yet further insights, opening up a more fundamental understanding of the nature of reality - for the individuals involved, and - for humanity as a whole. | ||
== Ongoing Sub-Projects == | |||
* [[The Road to Reality Study Notes|Studying the Tome]] - The Tome can be intimidating. This problem can be solved 1.) by creating resources that make it easier to digest its content and 2.) by going through the chapters together. | |||
* [[Annotating the Wall]] - The goal is to provide understandable explanations for all concepts shown on the Wall. | |||
* [[Animating the Wall]] - The goal is to make the wall more inviting and the symbols on it less cryptic. | |||
* [[Defacing the Wall]] - How can the wall be improved? | |||
* [[Decoding the Graph-Wall-Tome Connection]] - What are the common themes that appear in the Graph, the Wall, and the Tome? What do they hint at? | |||
* [[Editing the Graph]] - The goal is to create an updated version of the Graph since there are several small aspects of it that can and should be improved. | |||
* [[Geometry|Geometry Project]] - The aim is to create and collect resources related to Frederic P. Schuller's lecture series titled "Lectures on Geometrical Anatomy of Theoretical Physics" that provides a great introduction to geometrical concepts that are essential for the Graph, Wall, Tome project. | |||
* [[Holonomy Project]] - The goal is to create visualizations for the effect known as "holonomy", whereby parallel transporting a vector around a loop in a curved space leads to the vector changing upon returning to the start of the loop. How/how much the vector changes orientation/position in space is the holonomy of that loop in that space. This effect reveals deep information about the curvature of the space itself. | |||
== Eric Weinstein's Prompt == | == Eric Weinstein's Prompt == | ||
<blockquote> | <blockquote style="width:500px"> | ||
A request: Try to draw the lines through the three. View it as a unified idea:<br> | A request: <br> | ||
Try to draw the lines through the three. View it as a unified idea:<br> | |||
The paragraph gets edited.<br> | The paragraph gets edited.<br> | ||
The wall gets defaced and grafittied.<br> | The wall gets defaced and grafittied.<br> | ||
| Line 38: | Line 48: | ||
</blockquote> | </blockquote> | ||
== The Graph, The Wall, The Tome == | |||
===The Graph=== | |||
[[file:The-graph.png|right|class=shadow|350px]] | |||
The Graph is a paragraph (at the bottom of page 20) from Edward Witten's paper [https://cds.cern.ch/record/181783/files/cer-000093203.pdf Physics and Geometry]: | |||
<blockquote> | <blockquote style="width:850px"> | ||
If one wants to | If one wants to summarize our knowledge of physics in the briefest possible terms, there are three really fundamental observations: | ||
(i) Spacetime is a pseudo-Riemannian manifold $$M$$, endowed with a metric tensor and governed by geometrical laws. | (i) Spacetime is a pseudo-Riemannian manifold $$M$$, endowed with a metric tensor and governed by geometrical laws. | ||
(ii) Over M is a vector bundle $$X$$ with a | (ii) Over $$M$$ is a vector bundle $$X$$ with a non-abelian gauge group $$G$$. | ||
(iii) Fermions are sections of $$(\hat{S}{+} \otimes | (iii) Fermions are sections of $$(\hat{S}_{+} \otimes V_{R}) \oplus (\hat{S}_{-} \otimes V_{\tilde{R}})$$. $$R$$ and $$\tilde{R}$$ are not isomorphic; their failure to be isomorphic explains why the light fermions are light and presumably has its origins in representation difference $$\Delta$$ in some underlying theory. | ||
All of this must be supplemented with the understanding that the geometrical laws obeyed by the metric tensor, the gauge fields, and the fermions are to be interpreted in quantum mechanical terms. | All of this must be supplemented with the understanding that the geometrical laws obeyed by the metric tensor, the gauge fields, and the fermions are to be interpreted in quantum mechanical terms. | ||
</blockquote> | </blockquote> | ||
An updated version of the Graph can be found [[Editing_the_Graph|here]]. | |||
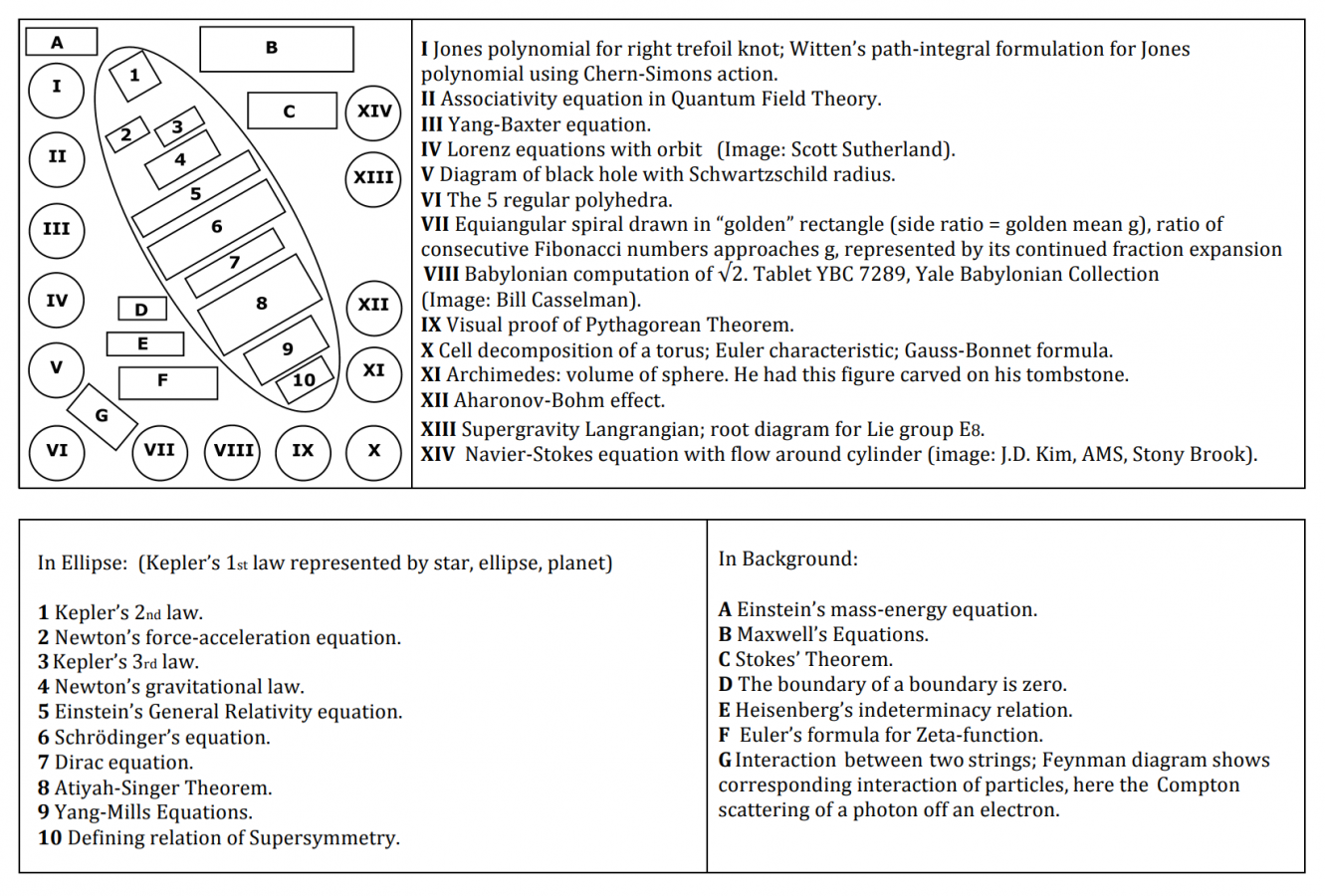
== The | ===The Wall=== | ||
[ | The following [http://www.math.stonybrook.edu/~tony/scgp/wall-story/wall-story.html image is carved into a wall at Stony Brook University]. It contains many of the most fundamental equations of physics, providing a formulaic representation of all reality. | ||
<div style="text-align: center;">'''[https://dev.theportal.dev/wall/ click here for an interactive version of the Wall].'''</div> | |||
<gallery mode="packed" heights=600px> | |||
File:Newwall.png|center|class=shadow|400px|The Wall | |||
File:Key-to-wall.png|center|class=shadow|400px|Explanations for the Wall | |||
</gallery> | |||
=== The Tome === | |||
[[File:The-tome.png|right|class=shadow|150px]] | |||
The Tome is the book Road to Reality by Roger Penrose which contains a comprehensive account of the physical universe. To gain an understanding and intuition for the information contained in 'The Graph', and 'The Wall', reading this book will provide a great head-start. With 34 chapters spread over 1000 pages, including diagrams, equations, and descriptions, there are multiple avenues for understanding all concepts. | |||
* ISBN: 978-0679776314 | * ISBN: 978-0679776314 | ||
* [https://www.amazon.com/Road-Reality-Complete-Guide-Universe/dp/0679776311 Road to Reality by Roger Penrose | * [https://www.amazon.com/Road-Reality-Complete-Guide-Universe/dp/0679776311 Road to Reality by Roger Penrose on Amazon] | ||
* Purchase the book somehow, then get the [https://www.academia.edu/351112/The_Road_to_Reality_Sir_Roger_Penrose PDF here] | |||
* There appears to be a [https://www.amazon.com/Road-Reality-Complete-Guide-Universe-ebook/dp/B01BS7NTA6 Kindle Edition] that isn't available in the US. If anyone in the community has a way to get a Kindle version of the book, please add it here. | * There appears to be a [https://www.amazon.com/Road-Reality-Complete-Guide-Universe-ebook/dp/B01BS7NTA6 Kindle Edition] that isn't available in the US. If anyone in the community has a way to get a Kindle version of the book, please add it here. | ||
* | * [https://discord.gg/3xgrNwJ The Portal Book Club] - We have a weekly group that meets to talk about this book. Come join us in Discord! | ||
Study notes for the Tome can be found [[The_Road_to_Reality_Study_Notes|here]]. | |||
Reference material by chapter can be found [[The Road to Reality|here]]. | |||
== Project | == Further Project Ideas== | ||
* Organize expeditions - (guided or unguided) tours through the portal and into the wonderful world we call physics. Intellectual tourism. | |||
* Create/assemble resources that provide a geometric intuition for the equations and principles of fundamental physics - Geometric interpretations are most amenable to being visually represented. An example, is shown [[Example Visualization|here]]. | |||
* Create [[Accelerators:|Accelerators: 2 minute guides to fundamental principles.]] | |||
* Create/assemble resources that allow uninitiated to quickly and easily get up to speed with state of the project. | |||
* Create/assemble resources that provide analogies for more complex principles - to demonstrate a key feature of the principle. | |||
* Annotate/colorize the most important equations | |||
* Publish discussions and comments on chapters of the Tome. | |||
* Publish study guide for the Tome. | |||
* Publish roadmaps for navigating through the Tome. | |||
* Create dependency graphs for chapters of the Tome. | |||
* Create expandable version of the Graph, i.e. multiple versions of the Graph that reveal more and more details. | |||
* Create fully-fledged learning path like [https://github.com/bmorelli25/Become-A-Full-Stack-Web-Developer] | |||
== Resources & References == | == Resources & References == | ||
* [https://drive.google.com/open?id=1sB_LTltdq8J6mIKyPRaHQWKEuLk0ZXuwYQZb78BnNuk | * Files related to the projected can be found in a [https://drive.google.com/drive/folders/1yPZHTNy47jUpmD-RMRCVtitfD-gQBRhP Google Drive Folder]. | ||
* [https://drive.google.com/open?id=1sB_LTltdq8J6mIKyPRaHQWKEuLk0ZXuwYQZb78BnNuk List of Tasks related to the Project] (no longer up to date) | |||
* [https://www.dropbox.com/s/xdickldblj574mf/eric%20wall%20-%20tome%20-%20graph.m4a?dl=0| Recording of original call w/ Eric] | * [https://www.dropbox.com/s/xdickldblj574mf/eric%20wall%20-%20tome%20-%20graph.m4a?dl=0| Recording of original call w/ Eric] | ||
* | * [[Eric’s Most Important Set of Books]] | ||
* [https://physicstravelguide.com/ The Physics Travel Guide] | * [https://physicstravelguide.com/ The Physics Travel Guide] - a didactic Wiki that explains math and physics concepts in three levels of difficulty. | ||
* [https://github.com/rossant/awesome-math Awesome Math] - a curated list of useful math resources. | |||
* Information about the GWT project were first collected in a Google Doc titled [https://docs.google.com/document/d/1Bo5ny0UyC8gEHiAaDR2Al2OSGscUWPS8NFI-hvB1z4o/edit?pli=1 Graph, Wall, Tome - Problem Solving]. | * Information about the GWT project were first collected in a Google Doc titled [https://docs.google.com/document/d/1Bo5ny0UyC8gEHiAaDR2Al2OSGscUWPS8NFI-hvB1z4o/edit?pli=1 Graph, Wall, Tome - Problem Solving]. | ||
* [https://www.youtube.com/playlist?list=PL5TiDYF_g45BA3abSyNl7M4pFzihZdoHT Relevant conversations with Eric on The Portal Discord Server] | |||
* [https://www.youtube.com/playlist?list=PL5TiDYF_g45BA3abSyNl7M4pFzihZdoHT | |||
* [https://www.youtube.com/playlist?list=PL5TiDYF_g45Az5qgAP5Lj8Y3qKPSib1eP Misc recordings on The Portal Server for project and other notable conversations] | * [https://www.youtube.com/playlist?list=PL5TiDYF_g45Az5qgAP5Lj8Y3qKPSib1eP Misc recordings on The Portal Server for project and other notable conversations] | ||
[[Category:Graph, Wall, Tome]] | |||
[[Category:Projects]] | |||
Revision as of 08:46, 31 July 2020
Fundamental physics is an unknown world to most people. Equations, symbols, and incomprehensible terms abound, and unless you've studied post-grad mathematics and physics, this world is inaccessible to you. Although there are several great resources to map the way toward complete understanding. Most people will not undertake the journey to understand the source code to the world that we all inhabit.
The goal of the Graph, Wall, Tome project is to solve this problem by building a portal anyone can use to travel to the amazing world that we call fundamental physics.
The name of the project stems from the observation that there are three resources that themselves contain all that you need for an almost complete understanding of the world.
- The Graph - A paragraph written by Edward Witten
- The Wall - The iconic wall of Stony Brook University
- The Tome - The book 'The Road to Reality' by Roger Penrose
These resources are available to everyone, but will be sought by almost none. A goal of the Graph, Wall, Tome project is to convert these resources into a medium that can be widely disseminated, and which can not be ignored.
This project will require bi-directional information transfer, and the minds of people with many different aptitudes.
- We need mathematicians, topologists, geometers, and physicists to understand these resources, and all of their implications.
- We need explainers and educators, to convey this information to a wider audience, and
- We need artists, linguists, and programmers to create intuitive visualisations.
The Portal will create a community of people, working together to achieve these aims.
Success will generate yet further insights, opening up a more fundamental understanding of the nature of reality - for the individuals involved, and - for humanity as a whole.
Ongoing Sub-Projects
- Studying the Tome - The Tome can be intimidating. This problem can be solved 1.) by creating resources that make it easier to digest its content and 2.) by going through the chapters together.
- Annotating the Wall - The goal is to provide understandable explanations for all concepts shown on the Wall.
- Animating the Wall - The goal is to make the wall more inviting and the symbols on it less cryptic.
- Defacing the Wall - How can the wall be improved?
- Decoding the Graph-Wall-Tome Connection - What are the common themes that appear in the Graph, the Wall, and the Tome? What do they hint at?
- Editing the Graph - The goal is to create an updated version of the Graph since there are several small aspects of it that can and should be improved.
- Geometry Project - The aim is to create and collect resources related to Frederic P. Schuller's lecture series titled "Lectures on Geometrical Anatomy of Theoretical Physics" that provides a great introduction to geometrical concepts that are essential for the Graph, Wall, Tome project.
- Holonomy Project - The goal is to create visualizations for the effect known as "holonomy", whereby parallel transporting a vector around a loop in a curved space leads to the vector changing upon returning to the start of the loop. How/how much the vector changes orientation/position in space is the holonomy of that loop in that space. This effect reveals deep information about the curvature of the space itself.
Eric Weinstein's Prompt
A request:
Try to draw the lines through the three. View it as a unified idea:
The paragraph gets edited.
The wall gets defaced and grafittied.
The Sacred Tome gets Re-Written
But follow the skeins through each.
The graph points to the wall.
And the wall to the Tome.
And the Tome leads to the Search.
The Graph, The Wall, The Tome
The Graph
The Graph is a paragraph (at the bottom of page 20) from Edward Witten's paper Physics and Geometry:
If one wants to summarize our knowledge of physics in the briefest possible terms, there are three really fundamental observations: (i) Spacetime is a pseudo-Riemannian manifold $$M$$, endowed with a metric tensor and governed by geometrical laws. (ii) Over $$M$$ is a vector bundle $$X$$ with a non-abelian gauge group $$G$$. (iii) Fermions are sections of $$(\hat{S}_{+} \otimes V_{R}) \oplus (\hat{S}_{-} \otimes V_{\tilde{R}})$$. $$R$$ and $$\tilde{R}$$ are not isomorphic; their failure to be isomorphic explains why the light fermions are light and presumably has its origins in representation difference $$\Delta$$ in some underlying theory. All of this must be supplemented with the understanding that the geometrical laws obeyed by the metric tensor, the gauge fields, and the fermions are to be interpreted in quantum mechanical terms.
An updated version of the Graph can be found here.
The Wall
The following image is carved into a wall at Stony Brook University. It contains many of the most fundamental equations of physics, providing a formulaic representation of all reality.
The Tome
The Tome is the book Road to Reality by Roger Penrose which contains a comprehensive account of the physical universe. To gain an understanding and intuition for the information contained in 'The Graph', and 'The Wall', reading this book will provide a great head-start. With 34 chapters spread over 1000 pages, including diagrams, equations, and descriptions, there are multiple avenues for understanding all concepts.
- ISBN: 978-0679776314
- Road to Reality by Roger Penrose on Amazon
- Purchase the book somehow, then get the PDF here
- There appears to be a Kindle Edition that isn't available in the US. If anyone in the community has a way to get a Kindle version of the book, please add it here.
- The Portal Book Club - We have a weekly group that meets to talk about this book. Come join us in Discord!
Study notes for the Tome can be found here.
Reference material by chapter can be found here.
Further Project Ideas
- Organize expeditions - (guided or unguided) tours through the portal and into the wonderful world we call physics. Intellectual tourism.
- Create/assemble resources that provide a geometric intuition for the equations and principles of fundamental physics - Geometric interpretations are most amenable to being visually represented. An example, is shown here.
- Create Accelerators: 2 minute guides to fundamental principles.
- Create/assemble resources that allow uninitiated to quickly and easily get up to speed with state of the project.
- Create/assemble resources that provide analogies for more complex principles - to demonstrate a key feature of the principle.
- Annotate/colorize the most important equations
- Publish discussions and comments on chapters of the Tome.
- Publish study guide for the Tome.
- Publish roadmaps for navigating through the Tome.
- Create dependency graphs for chapters of the Tome.
- Create expandable version of the Graph, i.e. multiple versions of the Graph that reveal more and more details.
- Create fully-fledged learning path like [1]
Resources & References
- Files related to the projected can be found in a Google Drive Folder.
- List of Tasks related to the Project (no longer up to date)
- Recording of original call w/ Eric
- Eric’s Most Important Set of Books
- The Physics Travel Guide - a didactic Wiki that explains math and physics concepts in three levels of difficulty.
- Awesome Math - a curated list of useful math resources.
- Information about the GWT project were first collected in a Google Doc titled Graph, Wall, Tome - Problem Solving.
- Relevant conversations with Eric on The Portal Discord Server
- Misc recordings on The Portal Server for project and other notable conversations