Holonomy Project: Difference between revisions

	Holonomy Project
Information
Topic	Graph, Wall, Tome
Leader	EricRWeinstein#6876
Links
	All Projects

Latest revision as of 19:00, 6 April 2024

A visualization of the effect known as "holonomy", whereby parallel transporting a vector around a loop in a curved space leads to the vector changing upon returning to the start of the loop. How/how much the vector changes orientation/position in space is the holonomy of that loop in that space. This effect reveals deep information about the curvature of the space itself.

Wait for Further News from Eric

Goals[edit]

Visualize holonomy to develop public intuition of the concept.

Demo[edit]

@@ Line 1: / Line 1: @@
-== Title ==
+{{InfoboxProject
-Holonomy Project
+|project=Holonomy Project
+|image=[[File:Holonomy.png]]
+|topic=[[Graph, Wall, Tome]]
+|leader=EricRWeinstein#6876
+|startdate=
+|customlabel1=
+|customdata1=
+|customlabel2=
+|customdata2=
+|customlabel3=
+|customdata3=
+|customlabel4=
+|customdata4=
+|link1title=
+|link1=
+|link2title=
+|link2=
+|link3title=
+|link3=
+|link4title=
+|link4=
+}}
-== Project Manager ==
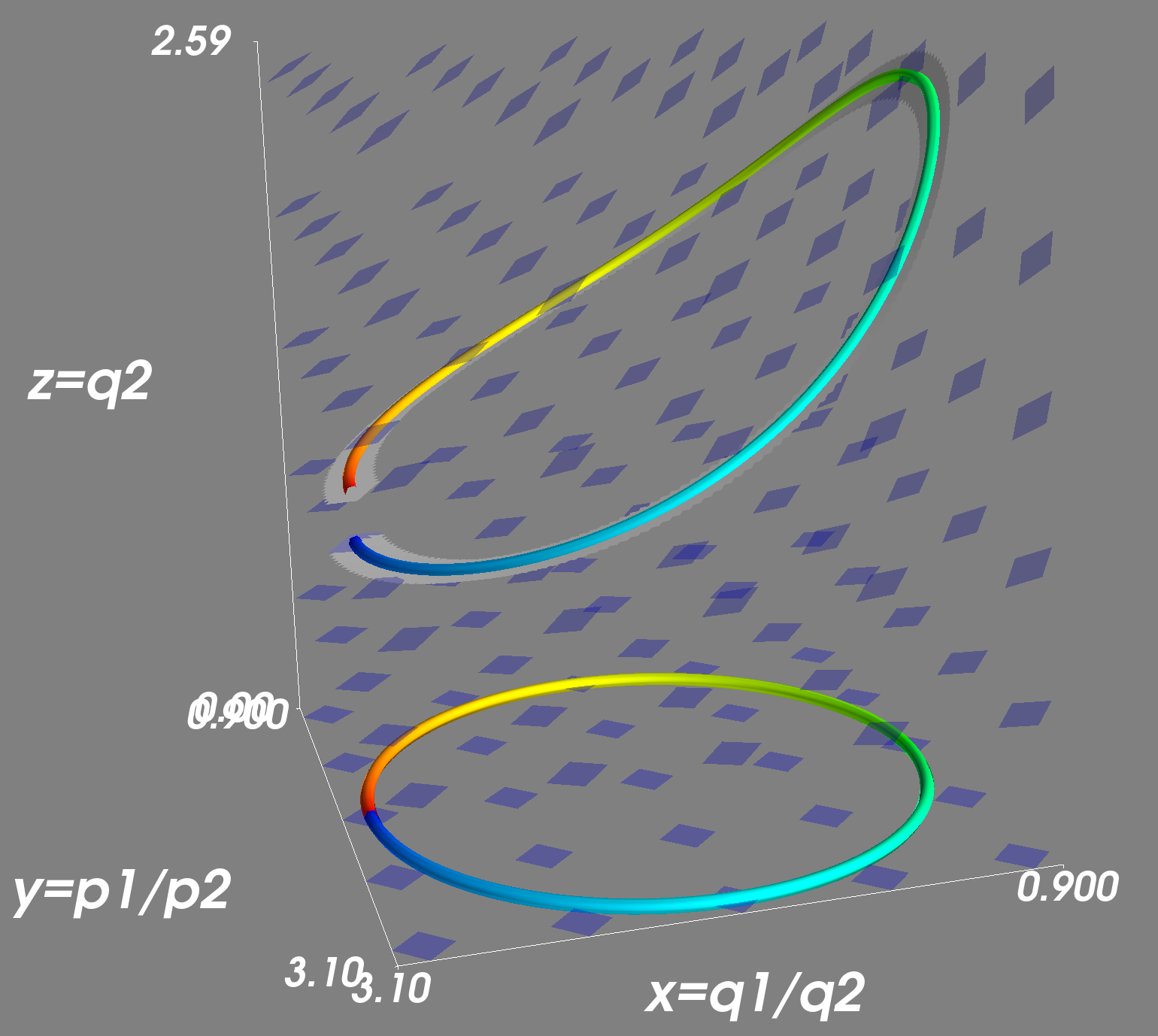
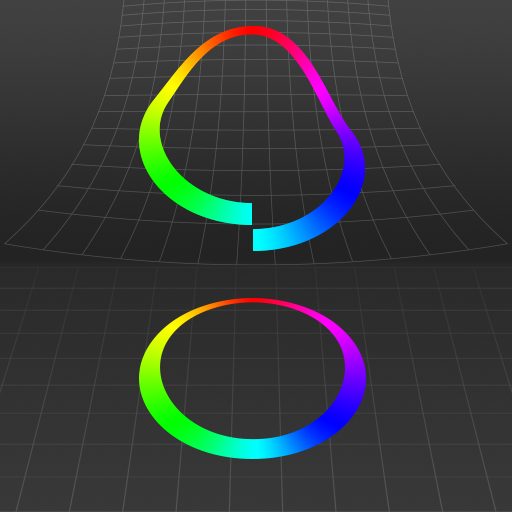
+A visualization of the effect known as "holonomy", whereby parallel transporting a vector around a loop in a curved space leads to the vector changing upon returning to the start of the loop. How/how much the vector changes orientation/position in space is the holonomy of that loop in that space. This effect reveals deep information about the [https://en.wikipedia.org/wiki/Curvature curvature] of the space itself.
-serenedesiree#0956
-== Team Members ==
+<span class="highlight">Wait for Further News from Eric</span>
-* serenedesiree#0956 - Project Lead
-* Tim FH#7940 - Mathematics Lead
-* Ben C#7492 - Programming Lead
-== Prod URL ==
+== Goals ==
-TBD
+* Visualize holonomy to develop public intuition of the concept.
-== Dev URL ==
+== Demo ==
-TBD
-== GitHub URL ==
+{{#widget:YouTube|id=fmDWCQs1bGI}}
-https://github.com/serenedesiree/Models (private)
-== Documentation URL ==
+<div class="max-width">
-https://github.com/serenedesiree/Models/blob/master/README.md (private)
+https://theportal.wiki/images/7/7b/Holonomy_Example_-1.png
+</div>
-== Description ==
-[Programming Lead's Best Attempt Effort] Interactive demos highlighting the concept of [https://en.wikipedia.org/wiki/Holonomy holonomy]: where a calm ("[https://en.wikipedia.org/wiki/Parallel_transport parallel transport]"), round trip path traveled following "straightest" paths ([https://en.wikipedia.org/wiki/Geodesic geodesics]) reveals deep information about the [https://en.wikipedia.org/wiki/Curvature curvature] of the space itself.
-== Long Description ==
-[Programming Lead's Best Stab]
-Gauge theory allows us to map from one space to another, essentially allowing exploration in the second space via traversing the original space. The position in the original space sets the foundations and assumptions of the second space, and by allowing that position to vary, we can move beyond fixed assumptions (such as, preferences are fixed in computing the consumer price index in Economics) to a mathematics that expresses the true underlying richness available across all of Physics, Economics, and other fields.
-This project provides a suite of interactive visualizations, aiming to share intuitions about the core concepts that are gatekeepers to understanding Gauge theory: multi-variable calculus, curvature, fiber bundles, and fibration. Intuition is built by implementing these concepts in things we can see and manipulate: 2D and 3D objects.
-Currently, we have a Python demo that shows how we can map from a 2D space into 5D: a 3D space with 2D vectors at each point. The visualization follows the  2D original space (x and y plane) as it varies in time, and shows the total amount of curvature (holonomy; z plane) experienced by a special kind of round-trip in the mapped space. Attached at each point, it also shows the curvature of the output space (otherwise, not visualized) associated with that point, to give a sense of how curvature is generating the holonomy measured at each point along the original space.
-== Screenshots ==
-[[File:Holonomy Example -1.png|thumb]]
-== Cover Image ==
-https://theportal.wiki/images/f/f5/Holonomy.png
+__NOTOC__
+[[Category:Archive]]
+[[Category:Stalled]]
 [[Category:Projects]]
-[[Category:Projects Needing a Cover Image]]
+[[Category:Graph, Wall, Tome]]
-__NOTOC__