Chapter 2: An ancient theorem and a modern question
Description goes here.
Community Explanations[edit]
Translation[edit]
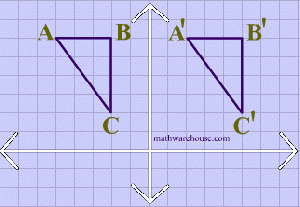
In Euclidean geometry, a translation is a geometric transformation that moves every point of a figure or a space by the same distance in a given direction.
Exponents[edit]
Exponents can be thought of as repeated multiplication, meaning:
[math]\displaystyle{ 2^3 = 2 \cdot 2 \cdot 2 }[/math]
and:
[math]\displaystyle{ 2^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 }[/math]
Multiplying these together we also see that:
[math]\displaystyle{ 2^3 \cdot 2^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 2^8 }[/math]
This is known as the additive property of exponentiation. It can be written as:
[math]\displaystyle{ 2^3 \cdot 2^5 = 2^{3+5} }[/math]
Or more generally:
[math]\displaystyle{ 2^a \cdot 2^b = 2^{a+b} }[/math]
Now, you may notice that this doesn't help if we are interested in numbers like [math]\displaystyle{ 2^{\frac{1}{2}} }[/math] or [math]\displaystyle{ 2^{-1} }[/math]. These cases are covered in the recommended section if you are interested but are not strictly necessary for understanding this chapter.
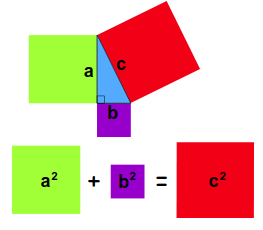
Pythagorean Theorem [math]\displaystyle{ a^2 + b^2 = c^2 }[/math][edit]
For any right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Here are some animated proofs as well as a quiz to test your understanding.
Euclidian Geometry[edit]
This is the fancy name for the basic geometry we are familiar with where parallel lines do not intersect. The rules or "postulates" of Euclidian geometry are as follows.
Euclidian Postulates[edit]
- A straight line segment can be drawn joining any two points.
- Any straight line segment can be extended indefinitely in a straight line.
- Given any straight line segment, a circle can be drawn having that segment as its radius.
- All right angles are congruent.
- If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. This postulate is equivalent to what is known as the parallel postulate.
A good video explaining these postulates as well as what postulates are can be found here.
Euclid's fifth postulate cannot be proven as a theorem (by assuming only the first four), although this was attempted by many people. Euclid himself used only the first four postulates ("absolute geometry") for the first 28 propositions of the Elements, but was forced to invoke the parallel postulate on the 29th. In 1823, Janos Bolyai and Nicolai Lobachevsky independently realized that entirely self-consistent "non-Euclidean geometries" could be created in which the parallel postulate did not hold. (Gauss had also discovered but suppressed the existence of non-Euclidean geometries.)
Radians and [math]\displaystyle{ \pi }[/math][edit]
[math]\displaystyle{ \pi }[/math] is introduced in the books as the sum of all angles of a triangles, which is [math]\displaystyle{ 180^\circ }[/math]. This might be confusing to those who know that [math]\displaystyle{ \pi = 3.14 \cdots }[/math].
The explanation for this is simple. [math]\displaystyle{ \pi }[/math] is simply used as a shorthand for [math]\displaystyle{ \pi R }[/math] where [math]\displaystyle{ R }[/math] stands for radian. An arc of a circle with the same length as the radius of that circle subtends an angle of 1 radian (roughly 57.29). Adding three radians together brings you almost 180 degrees around. [math]\displaystyle{ \pi }[/math] radians brings you exactly 180 degrees around. The circumference subtends an angle of [math]\displaystyle{ 2\pi }[/math]. To summarize: [math]\displaystyle{ 1 Radian = 1R = 57.29^\circ }[/math]: [math]\displaystyle{ \pi \cdot 57.29 = \pi r = 180^\circ }[/math]
So just remember, [math]\displaystyle{ \pi = 180^\circ }[/math]. Further explanations are given in the preliminaries section.
Representational Models[edit]
- Conformal Disk (Beltrami-Poincare)
- Projective (Beltrami-Klein)
- Hyperboloid (Mindowski-Lorenz)
Geodesic[edit]
A geodesic is a curve representing the shortest path between two points in a space. It is a generalization of the notion of a "straight line". In a "flat" space, the straight line is indeed the shortest distance between two points, but in a curved space, this no longer holds true; the shortest distance between two points inherits some of the curvature from the space in which it exists. Geodesics are well explained in the videos pertaining the hyperbolic geometry in the essential section.
Hyperbolic Geometry[edit]
A type of geometry which can emerge when the fifth postulate is no longer taken to be true. Objects like triangles obey different rules in this type of geometry. For instance, hyperbolic triangles have angles which sum to less than [math]\displaystyle{ \pi }[/math] radians. In fact, we have we have a triangle with an area represented by [math]\displaystyle{ \triangle }[/math] and three angles represented by [math]\displaystyle{ \alpha, \beta, \gamma }[/math] then by the Johann Heinrich Lambert formula:
[math]\displaystyle{ \pi - (\alpha + \beta + \gamma) = C \triangle }[/math]
where [math]\displaystyle{ C }[/math] is just some constant determined by the units by which we measure a give length or area. The units we use can always be chosen such that [math]\displaystyle{ C=1 }[/math].
In contrast to euclidean geometry where the angels of a triangle alone don’t tell you anything about its size - in hyperbolic geometry if you know the sum of the angels of a triangle, you can calculate its area using the formula above.
Preliminaries[edit]
- Know how to visually represent addition, subtraction, multiplication, and powers
- Know what squares (powers of two) and square roots are
- Know what logarithms are
- Know what an equation and the solution of an equation is (note that an equation can have more than one solution!)
- Now tie it all together
- And quick a introduction to radians
Essential[edit]
- An addictive puzzle game where you do Euclidean constructions
- Follow a steppable motion graphic that proves the Pythagorean theorem
- Squaring a triangle by Community Contributor @TimAlex
- A video game set on a hyperbolic plane
- HyperRogue for Android
- HyperRogue on Steam
- Hyperbolic geometry with Numberphile
Recommended[edit]
- Understanding fractional and negative powers
- A more in-depth description of the logarithms and exponents with applications
- The natural number and the natural logarithm
- For those who want an additional explanation of radians
- For those who want an additional explanation of radians and are mad about it
- Stereographic projections
- A spot of linear algebra
Further Exploration[edit]
- To understand what geometry really is
- The Four Pillars of Geometry by John Stillwell
- A guide through Euclid's Elements
- A more in depth introduction to linear algebra
- Linear Algebra Done Right by Sheldon Axler
Art[edit]
- Gorgeous hyperbolic art