Theory of Geometric Unity

• A first video presentation of the theory is available on Youtube
• A transcript of the talk is available here.
• Notes by the community on the talk are available in a Google Doc

Background

Cornerstones of modern physics

1. The Arena ([math]\displaystyle{ Xg_{\mu\nu} }[/math])	[math]\displaystyle{ R_{\mu\nu} - \frac{1}{2} Rg_{\mu\nu} + \Lambda g_{\mu\nu} = \left( \frac{1}{c^4} 8\pi GT_{\mu\nu}\right) }[/math]
2. [math]\displaystyle{ G }[/math] (non abelian) [math]\displaystyle{ SU(3) \times SU(2) \times U(1) }[/math]	[math]\displaystyle{ d_A^*F_A=J(\psi) }[/math]
3. Matter Antisymmetric, therefore light	[math]\displaystyle{ \partial_A \psi = m \psi }[/math]

Key guiding question: what are the compatibilities and incompatibilities on the geometric level before the theory is created quantum mechanical.

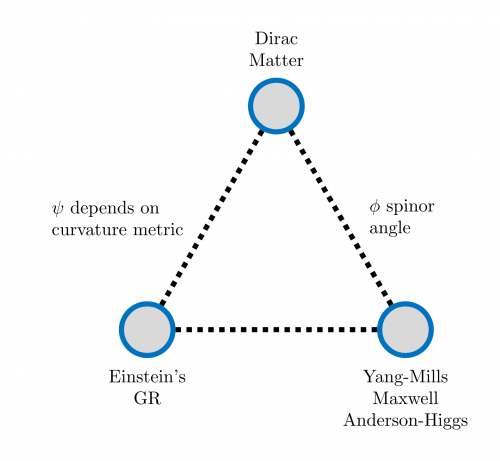
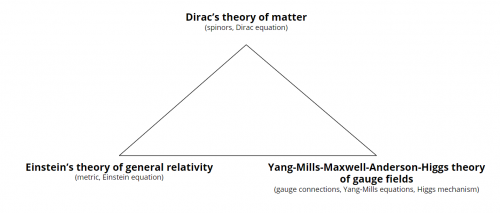
• From Einstein's general relativity, we take the Einstein projection of the curvature tensor of the Levi-Civita connection of the metric $P_E(F_A)$
• From Yang-Mills-Maxwell-Anderson-Higgs theory of gauge fields, we take the adjoint exterior derivative coupled to a connection $d^\star_A F_A$

Question: What if the $F_A$'s are the same in both contexts?

Then we're applying two different operators. The Einstein projection operator is zeroth order, it's destructive in the sense that it doesn't see the entire curvature tensor. The adjoint exterior derivative operator is inclusive but of first order.

Question: Is there any opportunity to combine these two operators?

Layman Explanation

a theory is like a newspaper story

• where/when -> space/time
• who/what -> fermions/bosons
• how/why -> rules/what generates the rules (equations and lagrangians)

Frequently Asked Questions

Please help answer these questions!

What will this theory predict?

When will Eric release the next part?

Why hasn't Eric gone through the normal scientific route? Arxiv.org? Academic journals?

Related existing theories

Causal Fermion Systems: [1]