Graph, Wall, Tome

The Assignment

There are 3 different pieces of the puzzle that Eric Weinstein pointed to during a call on Discord: graph, wall and tome. Please hold on to this information, that is they’re not public yet, until they come up in a dedicated future episode on The Portal. In the meantime, feel free to try to figure out how they fit together and what you can do with them in order to understand reality. Also, trying to answer the questions at the end helps you get started.

The Graph

The paragraph by Edward Witten as posted by Eric via Twitter.

However, there are 3 flaws with it:

• In (ii), “vector bundle X” should be changed to principal G-bundle.
• Also in (ii), “nonabelian gauge group G” should be changed to nonabelian structure group G.
• In (iii), R and R should be (complex) linear representations of G and so they are not equivalent.

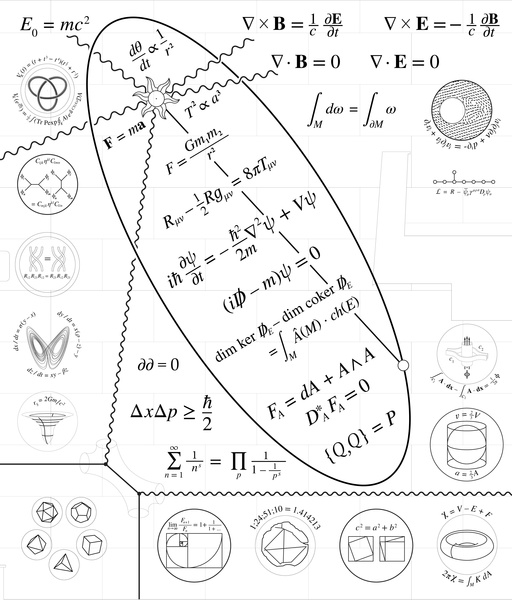
The Wall

Source

Eric talked about some of the important equations on the wall. There are 2 different recorded versions of the conversation if you want to listen to it.

The Tome

Road to Reality by Roger Penrose (2004) ISBN: 978-0679776314

Questions

Some questions Eric posed related to the assignment:

What is FA geometrically?

Atiyah-Singer index theorem

What is R and R geometrically?

Einstein field equaitions Einstein’s original publication, Die Feldgleichungen der Gravitation, in English

How do they relate?

Cohomologhy

What does this have to do with Penrose Steps?

• Penrose stairs
• Spino

We’ve heard Eric talk about Penrose stairs and spinors - essentially phenomena where you cannot return to the original state through a 360 degree rotation, but require a 720 degree rotation.

What are “Horizontal Subspaces” and what do they have to do with Vector Potentials or Gauge fields?

• Vertical and horizontal bundles
• Introduction to gauge theory
• Symmetry

From theplebistocrat:

Generally, we're wanting to understand how fermions arise from - or are embedded within / upon - topological "spaces" that have distinct rules which govern operations within those topological spaces, and then how those rules produce higher dimensional operations in corresponding spaces.

Just intuitively, and geometrically speaking, the image that I'm getting when describing all of this and trying to hold it in my head is the image of a sort of Penrose Tower of Babel, where the fundamental underlying structures reach upwards (but also downwards and inwards?) before reaching a critical rotation that corresponds to a collapse of structure into a higher dimensional fiber bundle.

But doesn't this require the symmetry break? How is left and right rotation in a subspace transformed into verticality? This is a crazy rabbit hole, friends. Keep your chins up. Let me know if this was helpful or leading astray.