Chapter 2: An ancient theorem and a modern question: Difference between revisions

From The Portal Wiki
No edit summary
No edit summary
Line 13: Line 13:
Exponents can be thought of as repeated multiplication, meaning:
Exponents can be thought of as repeated multiplication, meaning:


$$ 2^3 = 2 \cdot 2 \cdot 2 $$
<math> 2^3 = 2 \cdot 2 \cdot 2 </math>


and:  
and:  


$$ 2^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 $$
<math> 2^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 </math>


Multiplying these together we also see that:
Multiplying these together we also see that:


$$ 2^3 \cdot 2^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2  = 2^8$$
<math> 2^3 \cdot 2^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2  = 2^8</math>


This is known as the additive property of exponentiation. It can be written as:
This is known as the additive property of exponentiation. It can be written as:


$$ 2^3 \cdot 2^5 = 2^{3+5} $$
<math> 2^3 \cdot 2^5 = 2^{3+5} </math>


Or more generally:
Or more generally:


$$ 2^a \cdot 2^b = 2^{a+b} $$
<math> 2^a \cdot 2^b = 2^{a+b} </math>


Now, you may notice that this doesn't help if we are interested in numbers like \( 2^{\frac{1}{2}}\) or \(2^{-1}\). These cases are covered in the recommended section if you are interested but are not strictly necessary for understanding this chapter.
Now, you may notice that this doesn't help if we are interested in numbers like \( 2^{\frac{1}{2}}\) or \(2^{-1}\). These cases are covered in the recommended section if you are interested but are not strictly necessary for understanding this chapter.
Line 65: Line 65:


The explanation for this is simple. \( \pi \) is simply used as a shorthand for \( \pi R \) where \( R \) stands for radian. An arc of a circle with the same length as the radius of that circle subtends an '''angle of 1 radian''' (roughly 57.29). Adding three radians together brings you almost '''180 degrees''' around. \( \pi \) radians brings you ''exactly'' 180 degrees around. The circumference subtends an angle of \( 2\pi \). To summarize:
The explanation for this is simple. \( \pi \) is simply used as a shorthand for \( \pi R \) where \( R \) stands for radian. An arc of a circle with the same length as the radius of that circle subtends an '''angle of 1 radian''' (roughly 57.29). Adding three radians together brings you almost '''180 degrees''' around. \( \pi \) radians brings you ''exactly'' 180 degrees around. The circumference subtends an angle of \( 2\pi \). To summarize:
$$ 1 Radian = 1R = 57.29^\circ $$:
<math> 1 Radian = 1R = 57.29^\circ </math>:
$$ \pi \cdot 57.29 = \pi r = 180^\circ $$
<math> \pi \cdot 57.29 = \pi r = 180^\circ </math>


So just remember, \( \pi = 180^\circ \). Further explanations are given in the [[Preliminaries| preliminaries]] section.
So just remember, \( \pi = 180^\circ \). Further explanations are given in the [[Preliminaries| preliminaries]] section.
Line 85: Line 85:
A type of geometry which can emerge when the fifth postulate is no longer taken to be true. Objects like triangles obey different rules in this type of geometry. For instance, [https://en.wikipedia.org/wiki/Hyperbolic_triangle hyperbolic triangles] have angles which sum to '''less''' than \( \pi \) radians. In fact, we have we have a triangle with an area represented by \( \triangle \) and three angles represented by \( \alpha, \beta, \gamma \) then by the ''Johann Heinrich Lambert formula'':
A type of geometry which can emerge when the fifth postulate is no longer taken to be true. Objects like triangles obey different rules in this type of geometry. For instance, [https://en.wikipedia.org/wiki/Hyperbolic_triangle hyperbolic triangles] have angles which sum to '''less''' than \( \pi \) radians. In fact, we have we have a triangle with an area represented by \( \triangle \) and three angles represented by \( \alpha, \beta, \gamma \) then by the ''Johann Heinrich Lambert formula'':


$$ \pi - (\alpha + \beta + \gamma) = C \triangle $$
<math> \pi - (\alpha + \beta + \gamma) = C \triangle </math>


where \( C \) is just some constant determined by the ''units'' by which we measure a give length or area. The ''units'' we use can always be chosen such that \( C=1\).
where \( C \) is just some constant determined by the ''units'' by which we measure a give length or area. The ''units'' we use can always be chosen such that \( C=1\).

Revision as of 16:59, 19 February 2023

Description goes here.

<< Previous Chapter Table Of Contents next chapter >>

Community Explanations

Translation

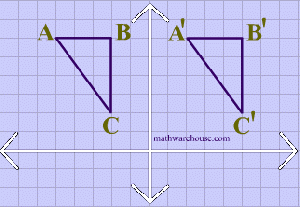
In Euclidean geometry, a translation is a geometric transformation that moves every point of a figure or a space by the same distance in a given direction.

Triangle ABC becomes triangle A'B'C' under the transformation called "translation".

Exponents

Exponents can be thought of as repeated multiplication, meaning:

[math]\displaystyle{ 2^3 = 2 \cdot 2 \cdot 2 }[/math]

and:

[math]\displaystyle{ 2^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 }[/math]

Multiplying these together we also see that:

[math]\displaystyle{ 2^3 \cdot 2^5 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 2^8 }[/math]

This is known as the additive property of exponentiation. It can be written as:

[math]\displaystyle{ 2^3 \cdot 2^5 = 2^{3+5} }[/math]

Or more generally:

[math]\displaystyle{ 2^a \cdot 2^b = 2^{a+b} }[/math]

Now, you may notice that this doesn't help if we are interested in numbers like \( 2^{\frac{1}{2}}\) or \(2^{-1}\). These cases are covered in the recommended section if you are interested but are not strictly necessary for understanding this chapter.

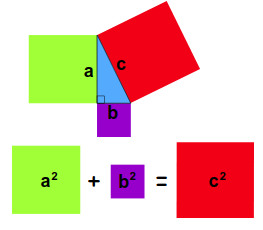
Pythagorean Theorem \( a^2 + b^2 = c^2 \)

For any right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

Here are some animated proofs as well as a quiz to test your understanding.

The squares with side lengths equal to the two shortest sides of the triangle have the same area as the square with side lengths equal to the longest side of the trangle.

Euclidian Geometry

This is the fancy name for the basic geometry we are familiar with where parallel lines do not intersect. The rules or "postulates" of Euclidian geometry are as follows.

Newton (1795–1805) 460 x 600 mm. Collection Tate Britain. Euclidean geometry is the study of mathematical objects that can be constructed by a straight edge and compass.

Euclidian Postulates

  1. A straight line segment can be drawn joining any two points.
  2. Any straight line segment can be extended indefinitely in a straight line.
  3. Given any straight line segment, a circle can be drawn having that segment as its radius.
  4. All right angles are congruent.
  5. If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. This postulate is equivalent to what is known as the parallel postulate.

A good video explaining these postulates as well as what postulates are can be found here.

Euclid's fifth postulate cannot be proven as a theorem (by assuming only the first four), although this was attempted by many people. Euclid himself used only the first four postulates ("absolute geometry") for the first 28 propositions of the Elements, but was forced to invoke the parallel postulate on the 29th. In 1823, Janos Bolyai and Nicolai Lobachevsky independently realized that entirely self-consistent "non-Euclidean geometries" could be created in which the parallel postulate did not hold. (Gauss had also discovered but suppressed the existence of non-Euclidean geometries.)

Euclid, coloured woodcut, 1584.

Radians and \( \pi \)

\( \pi \) is introduced in the books as the sum of all angles of a triangles, which is \( 180^\circ\). This might be confusing to those who know that \( \pi = 3.14 \cdots \).

The explanation for this is simple. \( \pi \) is simply used as a shorthand for \( \pi R \) where \( R \) stands for radian. An arc of a circle with the same length as the radius of that circle subtends an angle of 1 radian (roughly 57.29). Adding three radians together brings you almost 180 degrees around. \( \pi \) radians brings you exactly 180 degrees around. The circumference subtends an angle of \( 2\pi \). To summarize: [math]\displaystyle{ 1 Radian = 1R = 57.29^\circ }[/math]: [math]\displaystyle{ \pi \cdot 57.29 = \pi r = 180^\circ }[/math]

So just remember, \( \pi = 180^\circ \). Further explanations are given in the preliminaries section.

A radian of 1 is the angle which subtends an arc of length 1 on a unit circle, or equivalently, an arc length of r on a circle with radius r.

Representational Models

Geodesic

A geodesic is a curve representing the shortest path between two points in a space. It is a generalization of the notion of a "straight line". In a "flat" space, the straight line is indeed the shortest distance between two points, but in a curved space, this no longer holds true; the shortest distance between two points inherits some of the curvature from the space in which it exists. Geodesics are well explained in the videos pertaining the hyperbolic geometry in the essential section.

Hyperbolic Geometry

A type of geometry which can emerge when the fifth postulate is no longer taken to be true. Objects like triangles obey different rules in this type of geometry. For instance, hyperbolic triangles have angles which sum to less than \( \pi \) radians. In fact, we have we have a triangle with an area represented by \( \triangle \) and three angles represented by \( \alpha, \beta, \gamma \) then by the Johann Heinrich Lambert formula:

[math]\displaystyle{ \pi - (\alpha + \beta + \gamma) = C \triangle }[/math]

where \( C \) is just some constant determined by the units by which we measure a give length or area. The units we use can always be chosen such that \( C=1\).

In contrast to euclidean geometry where the angels of a triangle alone don’t tell you anything about its size - in hyperbolic geometry if you know the sum of the angels of a triangle, you can calculate its area using the formula above.

Hyperogue is a video game that takes place on the hyperbolic plane.

Preliminaries

Essential

Recommended

Further Exploration

Art

Conformal mappings on the Poincare disk by Paul Nylander
Retrieved from "https://theportal.wiki/index.php?title=Chapter_2:_An_ancient_theorem_and_a_modern_question&oldid=12924"