Fibonacci numbers

A tiling with squares whose side lengths are successive Fibonacci numbers: 1, 1, 2, 3, 5, 8, 13 and 21.

In mathematics, the Fibonacci numbers, commonly denoted [math]\displaystyle{ F_n }[/math], form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

[math]\displaystyle{ F_0=0,\quad F_1= 1, }[/math]

and

[math]\displaystyle{ F_n=F_{n-1} + F_{n-2}, }[/math]

for [math]\displaystyle{ n \gt 1 }[/math].

The beginning of the sequence is thus:

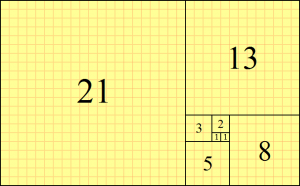
[math]\displaystyle{ 0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots }[/math]

Fibonacci numbers are named after Italian mathematician Leonardo of Pisa, later known as Fibonacci. In his 1202 book Liber Abaci, Fibonacci introduced the sequence to Western European mathematics, although the sequence had been described earlier in Indian mathematics as early as 200 BC in work by Pingala on enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths.

Mathematics

The ratio [math]\displaystyle{ \frac {F_n}{F_{n+1}} \ }[/math] approaches the golden ratio as [math]\displaystyle{ n }[/math] approaches infinity.

The Fibonacci numbers are the sums of the "shallow" diagonals (shown in red) of Pascal's triangle.

The Fibonacci numbers occur in the sums of "shallow" diagonals in Pascal's triangle.

[math]\displaystyle{ F_n = \sum_{k=0}^{\left\lfloor\frac{n-1}{2}\right\rfloor} \binom{n-k-1}{k} }[/math]

Resources:

• Golden spiral
• Fibonacci numbers