Classical Mechanics
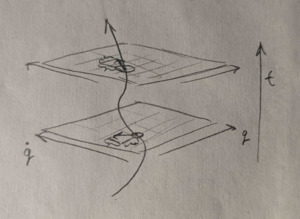
Classical Mechanics can be formulated directly and generally by applying calculus to trajectories/curves in space. For concreteness and an alternate presentation, we describe the formulation backwards from the first few pages of Landau's mechanics. Pictured on the side is a trajectory in one dimension [math]\displaystyle{ q(t) }[/math]. Since it is differentiable, we can plot the position and its derivative velocity [math]\displaystyle{ \dot{q}(t) }[/math] as a vector-valued function of time: [math]\displaystyle{ t_0 \rightarrow (q(t), \dot{q}(t)) }[/math] or points of the graph: [math]\displaystyle{ (q(t_0), \dot{q}(t_0), t_0) }[/math]. Now regarding the variables [math]\displaystyle{ q, \dot{q}, t }[/math] as mutually independent, there is a function called the Lagrangian [math]\displaystyle{ L(q, \dot{q}, t) }[/math] whereby the trajectory curve can be recovered, or the Lagrangian modified to give any other desired trajectory. In its most basic examples, it is a polynomial and constant in time:
Where m and k are constants. The equation determining the trajectory from any Lagrangian L is called the Euler Lagrange (EL) equation, position and velocity are now regarded as functions of time:
Computed in the particular example of a Lagrangian given previously. Regarding the position and velocity variables as functions of time again means that given a particular formula for a Lagrangian, the resulting Euler-Lagrange equation has the form of an ordinary differential equation whose solution is just the function [math]\displaystyle{ q(t) }[/math]. The partial derivatives of L with respect to position and velocity at each time indicate vectors in the constant-time planes as in the picture, that point in the direction of increase of L. Thus the Euler-Lagrange equation for motion in one dimension can be interpreted in the 3d geometric picture. The change in the velocity component of this vector as one moves up in time along the trajectory (e.g. it decreases) is the instantaneous value of the position component. This time derivative is in the case of when L is time independent, totally determined by the direction of the trajectory in the 3d graphed trajectory space at that time. Given an initial position and velocity at some time, this fixes the rest of the curve for future times, as it is constrained to follow the direction given by the EL equation at each time. In particular, this gives the endpoint at some chosen later time.
For the Lagrangian given, at initial condition [math]\displaystyle{ (1, 0, 0) }[/math] the solution is [math]\displaystyle{ cos(\sqrt{\frac{k}{m}}t) }[/math] which is the familiar oscillator of mass m and spring constant k. For higher dimensional and multi-particle systems, the generalization is from considering one EL equation to one for each dimension of position for each particle. For N particles in three dimensions, this gives 3N equations. Often, the Lagrangian is divided into two terms [math]\displaystyle{ L=T(\dot{q}_1, \dot{q}_2, \cdots, \dot{q}_{3N})-U(q_1, q_2, \cdots, q_{3N}) }[/math], with the term T depending only on the velocities is called the kinetic energy and U the potential energy. Now, we have an opportunity to analyze these terms and equations more generally. The derivatives [math]\displaystyle{ \frac{\partial L}{\partial \dot{q}_i} = \frac{\partial T}{\partial \dot{q}_i}, \quad i = 1, 2, \cdots, 3N }[/math] assembled as a vector are known as the momentum of the system. This another reason Lagrangians are powerful. Degrees of freedom need not come in multiples of three either.
For two masses rigidly joined at a fixed distance [math]\displaystyle{ l }[/math], the positions are described by only five coordinates. First, the three of one mass, then the two angles to choose a point on the sphere of radius [math]\displaystyle{ l }[/math] about the first mass, to fix the position of the second.
Letting the [math]\displaystyle{ q_i }[/math] coordinates be coordinates other than Cartesian, e.g. spherical coordinates for each particle, allows us to discuss linear and angular momentum on the same footing or momentum in any convenient coordinate system. Given [math]\displaystyle{ m_{1+((i-1)-(i-1)\,mod 3)/3} = m_k }[/math] as the mass of the k'th particle in order, in cartesian coordinates [math]\displaystyle{ T=\sum_{i=1}^{3N} \frac{1}{2}m_k \dot{q}^2_i }[/math] gives [math]\displaystyle{ \frac{\partial T}{\partial \dot{q}_i}=m_k \dot{q}_i=m_k v_i = p_i }[/math]. Similarly, the coordinate derivative gives [math]\displaystyle{ \frac{\partial L}{\partial q_i}=-\frac{\partial U}{\partial q_i} = F_i }[/math] which has the interpretation of force on the i'th coordinate. Then the i'th EL equation is expressed as [math]\displaystyle{ m_k \frac{d}{dt} v_i = m_k a_i= F_i }[/math] which is just Newton's second law. Indeed, all of Newton's laws can be derived from this formulation of motion, but to do so fully we need an equation using finite properties of the Lagrangian and not just an infinitesimal condition.
Supposing [math]\displaystyle{ q_i(t) }[/math] solves the EL equations for s degrees of freedom, we can analyze properties of the integral across finite time [math]\displaystyle{ S = \int_{t_1}^{t_2} L(q_1(t), \cdots, q_s(t), \dot{q}_1(t), \cdots, \dot{q}_s(t), t) dt }[/math], since substituting the trajectory gives a strict function of time. Integrals/primitives are often viewed as functions of the bounds of integration, however the perspective in mechanics is to make it a function of the trajectory. This means [math]\displaystyle{ S(q(-)) }[/math] with t suppressed to indicate it does not depend on time is a scalar function on an infinite dimensional space of paths. We want to understand its derivative, and thus when it has a minimum. There is an easy way to do this without thinking too hard about how to formulate what these spaces are, which we do in a later section to enhance this explanation. Also note that being a function of the trajectory (a functional) means that the underlying set of the trajectory in physical configuration space does not describe the motion completely, since the same path can be traced out by motion at different velocities implying the need for the parametrization by time. Parametrization-dependence is exploited further in differential geometry when defining tangent vectors on abstract manifolds.
In two dimensions, rather than infinite, the minimum of a function can be described by an equivalent condition to the derivative being 0. Let [math]\displaystyle{ F:\mathbb{R}^2\rightarrow \mathbb{R} }[/math]. Typically we would check the condition [math]\displaystyle{ \frac{\partial F(x_0,y_0)}{\partial x}=\frac{\partial F(x_0,y_0)}{\partial y}=0 }[/math] at some point [math]\displaystyle{ (x_0,y_0)\in \mathbb{R}^2 }[/math].