Fibonacci numbers: Difference between revisions
(Created page with "<div class="floatright" style="text-align: center"> center|class=shadow|300px </div> == Resources: == *[https://en.wikipedia.org/wiki/Golde...") |
(Initial Stub) |
||
| Line 1: | Line 1: | ||
<div | <div style="text-align: center; padding-right: 300"> | ||
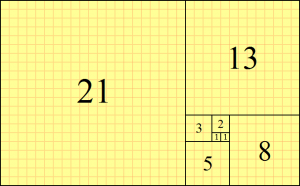
[[File: | [[File:34 21-FibonacciBlocks.png|right|300px|thumb|A tiling with squares whose side lengths are successive Fibonacci numbers: 1, 1, 2, 3, 5, 8, 13 and 21.]] | ||
</div> | </div> | ||
In mathematics, the '''Fibonacci numbers''', commonly denoted <math>F_n</math>, form a sequence, called the '''Fibonacci sequence''', such that each number is the sum of the two preceding ones, starting from 0 and 1. That is, | |||
:<math>F_0=0,\quad F_1= 1,</math> | |||
and | |||
:<math>F_n=F_{n-1} + F_{n-2},</math> | |||
for <math>n > 1</math>. | |||
The beginning of the sequence is thus: | |||
:<math>0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots</math> | |||
== Resources: == | == Resources: == | ||
Revision as of 03:07, 2 May 2020
In mathematics, the Fibonacci numbers, commonly denoted [math]\displaystyle{ F_n }[/math], form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,
- [math]\displaystyle{ F_0=0,\quad F_1= 1, }[/math]
and
- [math]\displaystyle{ F_n=F_{n-1} + F_{n-2}, }[/math]
for [math]\displaystyle{ n \gt 1 }[/math].
The beginning of the sequence is thus:
- [math]\displaystyle{ 0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots }[/math]