Lie group E8: Difference between revisions
(Created page with "<div class="floatright" style="text-align: center"> center|class=shadow|300px </div> From Wikipedia, the free encyclopedia In mathematics, E8 is any...") |
No edit summary |
||
| Line 11: | Line 11: | ||
== Discussion: == | == Discussion: == | ||
[[Category:Archive]] | |||
[[Category:Pages for Merging]] | |||
Revision as of 18:41, 7 October 2020
From Wikipedia, the free encyclopedia
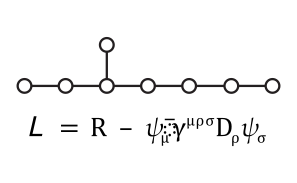
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8. The designation E8 comes from the Cartan–Killing classification of the complex simple Lie algebras, which fall into four infinite series labeled An, Bn, Cn, Dn, and five exceptional cases labeled E6, E7, E8, F4, and G2. The E8 algebra is the largest and most complicated of these exceptional cases.