Classical Mechanics: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| Line 18: | Line 18: | ||
Computed in the particular example of a Lagrangian given previously. Regarding the position and velocity variables as functions of time again means that given a particular formula for a Lagrangian, the resulting Euler-Lagrange equation has the form of an ordinary differential equation whose solution is just the function <math> q(t) </math>. The partial derivatives of L with respect to position and velocity at each time indicate vectors in the constant-time planes as in the picture, that point in the direction of increase of L. Thus the Euler-Lagrange equation for motion in one dimension can be interpreted in the 3d geometric picture. The change in the velocity component of this vector as one moves up in time along the trajectory (e.g. it decreases) is the instantaneous value of the position component. This time derivative is in the case of when L is time independent, totally determined by the direction of the trajectory in the 3d graphed trajectory space at that time. Given an initial position and velocity at some time, this fixes the rest of the curve for future times, as it is constrained to follow the direction given by the EL equation at each time. In particular, this gives the endpoint at some chosen later time. | Computed in the particular example of a Lagrangian given previously. Regarding the position and velocity variables as functions of time again means that given a particular formula for a Lagrangian, the resulting Euler-Lagrange equation has the form of an ordinary differential equation whose solution is just the function <math> q(t) </math>. The partial derivatives of L with respect to position and velocity at each time indicate vectors in the constant-time planes as in the picture, that point in the direction of increase of L. Thus the Euler-Lagrange equation for motion in one dimension can be interpreted in the 3d geometric picture. The change in the velocity component of this vector as one moves up in time along the trajectory (e.g. it decreases) is the instantaneous value of the position component. This time derivative is in the case of when L is time independent, totally determined by the direction of the trajectory in the 3d graphed trajectory space at that time. Given an initial position and velocity at some time, this fixes the rest of the curve for future times, as it is constrained to follow the direction given by the EL equation at each time. In particular, this gives the endpoint at some chosen later time. | ||
For the Lagrangian given, at initial condition <math> (1, 0, 0) </math> the solution is <math> cos(\sqrt{\frac{k}{m}}t) </math> which is the familiar oscillator of mass m and spring constant k. For higher dimensional and multi-particle systems, the generalization is from considering one EL equation to one for each dimension of position for each particle. For N particles in three dimensions, this gives 3N equations. | For the Lagrangian given, at initial condition <math> (1, 0, 0) </math> the solution is <math> cos(\sqrt{\frac{k}{m}}t) </math> which is the familiar oscillator of mass m and spring constant k. For higher dimensional and multi-particle systems, the generalization is from considering one EL equation to one for each dimension of position for each particle. For N particles in three dimensions, this gives 3N equations. Often, the Lagrangian is divided into two terms <math> T(\dot{q}_1, \dot{q}_2, \cdots, \dot{q}_{3N})-U(q_1, q_2, \cdots, q_{3N}) </math>, with the term T depending only on the velocities is called the kinetic energy and U the potential energy. | ||
Revision as of 14:28, 6 February 2024
Initial Lagrangian Framing
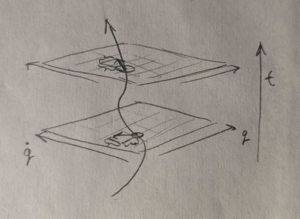
Classical Mechanics can be formulated directly and generally by applying calculus to trajectories/curves in space. For concreteness and an alternate presentation, we describe the formulation backwards from the first few pages of Landau's mechanics. Pictured on the side is a trajectory in one dimension [math]\displaystyle{ q(t) }[/math]. Since it is differentiable, we can plot the position and its derivative velocity [math]\displaystyle{ \dot{q}(t) }[/math] as a vector-valued function of time: [math]\displaystyle{ t_0 \rightarrow (q(t), \dot{q}(t)) }[/math] or points of the graph: [math]\displaystyle{ (q(t_0), \dot{q}(t_0), t_0) }[/math]. Now regarding the variables [math]\displaystyle{ q, \dot{q}, t }[/math] as mutually independent, there is a function called the Lagrangian [math]\displaystyle{ L(q, \dot{q}, t) }[/math] whereby the trajectory curve can be recovered, or the Lagrangian modified to give any other desired trajectory. In its most basic examples, it is a polynomial and constant in time:
[math]\displaystyle{ L = m*\frac{\dot{q}^2}{2}-k*\frac{q^2}{2} }[/math]
Where m and k are constants. The equation determining the trajectory from any Lagrangian L is called the Euler Lagrange (EL) equation, position and velocity are now regarded as functions of time:
[math]\displaystyle{ \frac{d}{dt} \frac{\partial L(q(t), \dot{q}(t), t)}{\partial \dot{q}}=\frac{\partial L(q(t), \dot{q}(t), t)}{\partial q},\quad m * \frac{d^2 q(t)}{dt^2}=-k*q(t) }[/math]
Computed in the particular example of a Lagrangian given previously. Regarding the position and velocity variables as functions of time again means that given a particular formula for a Lagrangian, the resulting Euler-Lagrange equation has the form of an ordinary differential equation whose solution is just the function [math]\displaystyle{ q(t) }[/math]. The partial derivatives of L with respect to position and velocity at each time indicate vectors in the constant-time planes as in the picture, that point in the direction of increase of L. Thus the Euler-Lagrange equation for motion in one dimension can be interpreted in the 3d geometric picture. The change in the velocity component of this vector as one moves up in time along the trajectory (e.g. it decreases) is the instantaneous value of the position component. This time derivative is in the case of when L is time independent, totally determined by the direction of the trajectory in the 3d graphed trajectory space at that time. Given an initial position and velocity at some time, this fixes the rest of the curve for future times, as it is constrained to follow the direction given by the EL equation at each time. In particular, this gives the endpoint at some chosen later time.
For the Lagrangian given, at initial condition [math]\displaystyle{ (1, 0, 0) }[/math] the solution is [math]\displaystyle{ cos(\sqrt{\frac{k}{m}}t) }[/math] which is the familiar oscillator of mass m and spring constant k. For higher dimensional and multi-particle systems, the generalization is from considering one EL equation to one for each dimension of position for each particle. For N particles in three dimensions, this gives 3N equations. Often, the Lagrangian is divided into two terms [math]\displaystyle{ T(\dot{q}_1, \dot{q}_2, \cdots, \dot{q}_{3N})-U(q_1, q_2, \cdots, q_{3N}) }[/math], with the term T depending only on the velocities is called the kinetic energy and U the potential energy.