Schwarzschild radius: Difference between revisions
No edit summary |
No edit summary |
||
| Line 8: | Line 8: | ||
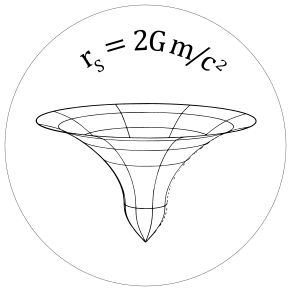
The Schwarzschild radius is given as | The Schwarzschild radius is given as | ||
<math> {r_{s}={\frac {2GM}{c^{2}}}}{\displaystyle r_{s}={\frac {2GM}{c^{2}}}}</math> | |||
where G is the gravitational constant, M is the object mass, and c is the speed of light. | where G is the gravitational constant, M is the object mass, and c is the speed of light. | ||
Latest revision as of 16:39, 19 February 2023
From Wikipedia, the free encyclopedia
The Schwarzschild radius (sometimes historically referred to as the gravitational radius) is a physical parameter that shows up in the Schwarzschild solution to Einstein's field equations, corresponding to the radius defining the event horizon of a Schwarzschild black hole. It is a characteristic radius associated with every quantity of mass. The Schwarzschild radius was named after the German astronomer Karl Schwarzschild, who calculated this exact solution for the theory of general relativity in 1916.
The Schwarzschild radius is given as
[math]\displaystyle{ {r_{s}={\frac {2GM}{c^{2}}}}{\displaystyle r_{s}={\frac {2GM}{c^{2}}}} }[/math]
where G is the gravitational constant, M is the object mass, and c is the speed of light.