Theory of Geometric Unity: Difference between revisions

Revision as of 14:17, 21 April 2020

A first video presentation of the theory is available on Youtube
A transcript of the talk is available here.
Notes by the community on the talk are available in a Google Doc

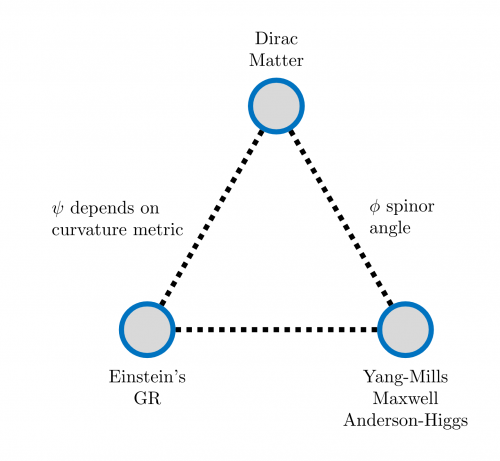
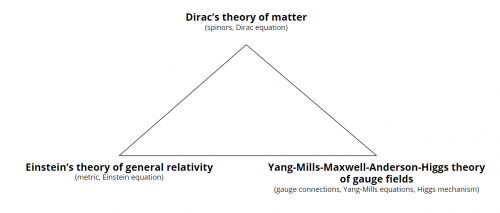
Background

Cornerstones of modern physics

1. The Arena ([math]\displaystyle{ Xg_{\mu\nu} }[/math])	[math]\displaystyle{ R_{\mu\nu} - \frac{1}{2} Rg_{\mu\nu} + \Lambda g_{\mu\nu} = \left( \frac{1}{c^4} 8\pi GT_{\mu\nu}\right) }[/math]
2. [math]\displaystyle{ G }[/math] (non abelian) [math]\displaystyle{ SU(3) \times SU(2) \times U(1) }[/math]	[math]\displaystyle{ d_A^*F_A=J(\psi) }[/math]
3. Matter Antisymmetric, therefore light	[math]\displaystyle{ \partial_A \psi = m \psi }[/math]

Key guiding question: what are the compatibilities and incompatibilities on the geometric level before the theory is created quantum mechanical.

From Einstein's general relativity, we take the Einstein projection of the curvature tensor of the Levi-Civita connection of the metric $$P_E(F_{\Delta^LC})$$
From Yang-Mills-Maxwell-Anderson-Higgs theory of gauge fields, we take the adjoint exterior derivative coupled to a connection $$d^\star_A F_A$$

Question: What if the $$F$$'s are the same in both contexts?

Then we're applying two different operators. The Einstein projection operator is zeroth order, it's destructive in the sense that it doesn't see the entire curvature tensor. The adjoint exterior derivative operator is inclusive but of first order.

Question: Is there any opportunity to combine these two operators?

A problem is that the hallmark of the Yang-Mills theory is the freedom to choose the data, the internal quantum numbers that give all the particles their personalities beyond the mass and the spin. We can allow the gauge group of symmetries to act on both sides of the equation, but the key problem is that: $$P_E(F_{\Delta^LC h}) \neq h^{-1} P_E(F_{\Delta^LC }) h $$. If I act on connections on the right and then take the Einstein projection, this is not equal to first taking the projection and then conjugating with the gauge action. So the problem is, is that the projection is based on the fact that you have a relationship between the intrinsic geometry. If this is an ad-valued two-form, the two-form portion of this and the adjoint portion of this are both associated to the structure group of the tangent bundle.

Layman Explanation

a theory is like a newspaper story

where/when -> space/time
who/what -> fermions/bosons
how/why -> rules/what generates the rules (equations and lagrangians)

Frequently Asked Questions

Please help answer these questions!

What will this theory predict?

When will Eric release the next part?

Why hasn't Eric gone through the normal scientific route? Arxiv.org? Academic journals?

Related existing theories

Causal Fermion Systems: [1]

@@ Line 31: / Line 31: @@
 '''Key guiding question:''' what are the compatibilities and incompatibilities on the geometric level before the theory is created quantum mechanical.
-* From Einstein's general relativity, we take the Einstein projection of the curvature tensor of the Levi-Civita connection of the metric $P_E(F_A)$
+* From Einstein's general relativity, we take the Einstein projection of the curvature tensor of the Levi-Civita connection of the metric $$P_E(F_{\Delta^LC})$$
-* From Yang-Mills-Maxwell-Anderson-Higgs theory of gauge fields, we take the adjoint exterior derivative coupled to a connection $d^\star_A F_A$
+* From Yang-Mills-Maxwell-Anderson-Higgs theory of gauge fields, we take the adjoint exterior derivative coupled to a connection $$d^\star_A F_A$$
-'''Question:''' What if the $F_A$'s are the same in both contexts?
+'''Question:''' What if the $$F$$'s are the same in both contexts?
 Then we're applying two different operators. The Einstein projection operator is zeroth order, it's destructive in the sense that it doesn't see the entire curvature tensor. The adjoint exterior derivative operator is inclusive but of first order.
 '''Question:''' Is there any opportunity to combine these two operators?
+A problem is that the hallmark of the Yang-Mills theory is the freedom to choose the data, the internal quantum numbers that give all the particles their personalities beyond the mass and the spin. We can allow the gauge group of symmetries to act on both sides of the equation, but the key problem is that: $$P_E(F_{\Delta^LC h}) \neq  h^{-1} P_E(F_{\Delta^LC }) h $$. If I act on connections on the right and then take the Einstein projection, this is not equal to first taking the projection and then conjugating with the gauge action. So the problem is, is that the projection is based on the fact that you have a relationship between the intrinsic geometry. If this is an ad-valued two-form, the two-form portion of this and the adjoint portion of this are both associated to the structure group of the tangent bundle.