The Road to Reality Study Notes
Each week The Road to Reality Book Club tackles a chapter of Sir Roger Penrose's Epic Tome. We use these meetings as an opportunity to write down the major points to be taken from our reading. Here we attempt to sum up what we believe Penrose was trying to convey and why. The hope is that these community-generated reading notes will benefit people in the future as they go on the same journey.
Chapters 1-16 focus on mathematical concepts while the later chapters use this background to describe the physical world.
- The Portal Book Club - We have a weekly group that meets to talk about this book. Come join us in Discord!
- Reference Material by Chapter on the Wiki
Chapter 1 The Roots of Science[edit]
1.1 The quest for the forces that shape the world[edit]
Understanding natural processes has been a common pursuit since the dawn of humanity. After many millennia of chaos and frustration, it was discovered that the regular movement of celestial bodies, such as the sun and moon, could be described mathematically. It became apparent that mathematics unlocked deep truths about the universe. Many people in ancient times allowed their imaginations to be carried away by their fascination with the subject, leading to mystical associations with mathematical objects. One famous example from the ancient Greeks is the association between Platonic solids and the basic elementary states of matter.
1.2 Mathematical truth[edit]
There was a need to define a more rigorous method for differentiating truth claims. The Greek philosopher Thales of Miletus (c. 625-547 BC) and Pythagoras of Samos (c. 572-497 BC) are considered to be the first to introduce the concept of mathematical proof. Developing a rigorous mathematical framework was central to the development of science. Mathematical proof allowed for much stronger statements to be made about relationships between the arithmetic of numbers and the geometry of physical space.
A mathematical proof is essentially an argument in which one starts from a mathematical statement, which is taken to be true, and using only logical rules arrives at a new mathematical statement. If the mathematician hasn't broken any rules then the new statement is called a theorem. The most fundamental mathematical statements, from which all other proofs are built, are called axioms and their validity is taken to be self-evident. Mathematicians trust that the axioms, on which their theorems depend, are actually true. The Greek philosopher Plato (c.429-347 BC) believed that mathematical proofs referred not to actual physical objects but to certain idealized entities. Physical manifestations of geometric objects could come close to the Platonic world of mathematical forms, but they were always approximations. To Plato the idealized mathematical world of forms was a place of absolute truth, but inaccessible from the physical world.
1.3 Is Plato's mathematical world "real"?[edit]
Penrose asks us to consider if the world of mathematics is in any sense real. He claims that objective truths are revealed through mathematics and that it is not a subjective matter of opinion. He uses Fermat's last theorem as a point to consider what it would mean for mathematical statements to be subjective. He shows that "the issue is the objectivity of the Fermat assertion itself, not whether anyone’s particular demonstration of it (or of its negation) might happen to be convincing to the mathematical community of any particular time". Penrose introduces a more complicated mathematical notion, the axiom of choice, which has been debated amongst mathematicians. He notes that "questions as to whether some particular proposal for a mathematical entity is or is not to be regarded as having objective existence can be delicate and sometimes technical". Finally he discusses the Mandelbrot set and claims that it exists in a place outside of time and space and was only uncovered by Mandelbrot. Any mathematical notion can be thought of as existing in that place. Penrose invites the reader to reconsider their notions of reality beyond the matter and stuff that makes up the physical world.
For further discussion from Penrose on this topic see Is Mathematics Invented or Discovered?
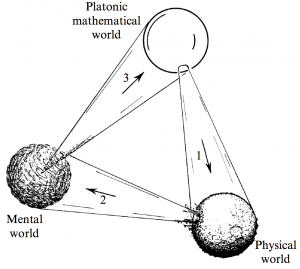
1.4 Three worlds and three deep mysteries[edit]
Penrose outlines his conception of three worlds:
- The Platonic Mathematical
- The Physical
- The Mental
as shown in figure 1.3. Connections between these worlds present a great number of mysteries. The main focus of the book is to explore the connection between mathematics and its use in describing the physical world. Note that only a small subset of the mathematical world is utilized in describing the physical world. The reason why mathematics can describe the physical world so accurately is unknown. Moving in the counter clockwise direction there is a mysterious connection between the physical world and that of the mind. He believes that there must be some basis of consciousness in physical reality, but it is still unknown. Finally there is the connection between the mental world and mathematics. Penrose believes that there is no mathematical notion beyond our mental construction. He highlights that this figure represents many of his prejudices and might upset some people. Maybe the connections from one world do not fully describe the other, or are incomplete. Penrose believes that not much progress can be made with respect to the mental world until we know much more about the physical world.
1.5 The Good, the True, and the Beautiful[edit]
The full conception of Plato's theory of forms was not limited to only mathematical notions. Mathematics was linked to the concept of Truth but Plato was also interested in the absolute idealized forms of Beauty and Good. Beauty plays an important role in many mathematical discoveries and is often used as a guide to the truth. Questions of morality are of less relevance in this context but are critical with respect to the mental world. Moral debates are outside of the scope of this book but must be considered as science and technology progress. Penrose notes that figure 1.3 has purposely been constructed to be paradoxical in the sense that each world is entirely encompassed by the next. He writes "There may be a sense in which the three worlds are not separate at all, but merely reflect, individually, aspects of a deeper truth about the world as a whole of which we have little conception at the present time."
Chapter 2 An ancient theorem and a modern question[edit]
2.1 The Pythagorean theorem[edit]
To explore the process of pursuing mathematical truth, Penrose outlines a few proofs of the Pythagorean theorem. The theorem can be stated as such, "For any right-angled triangle, the squared length of the hypotenuse [math]\displaystyle{ c }[/math] is the sum of the squared lengths of the other two sides [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] or in mathematical notation [math]\displaystyle{ a^2 + b^2 = c^2. }[/math]
There are hundreds of proofs of the Pythagorean theorem but Penrose chooses to focus on two. The first involves filling up a plane with squares of two different sizes. Then adding a second pattern on top of tiled squares connecting the centers of the larger original squares. By translating the tilted pattern to the corner of the large square and observing the areas covered by the pattern you can show that the square on the hypotenuse is equal to the sum of the squares on the other two sides. While the outlined proof appears reasonable there are some implicit assumptions made. For instance what do you mean when we say square? What is a right angle?
2.2 Euclid's postulates[edit]
Euclid of Alexandria, sometimes referred to as the "father of geometry", was one of the first people to attempt to outline and document the assumptions that went into his geometrical arguments. Euclid broke these assumptions into two categories, axioms which were self-evident, essentially definitions, and a set of five postulates which were less certain, but appeared true. Penrose outlines the first 4 postulates as:
- There is a (unique) straight line segment connecting any two points.
- There is an unlimited (continuous) extendibility of any straight line segment.
- There existence a circle with any centre and with any value for its radius.
- There is equality of all right angles.
Euclid was trying to establish the rules which govern his geometry. Some interesting ideas start to emerge such as the indefinitely extendible geometric plane and the concept of congruence. Penrose writes "In effect, the fourth postulate is asserting the isotropy and homogeneity of space, so that a figure in one place could have the ‘same’ (i.e. congruent) geometrical shape as a figure in some other place". Surprisingly Euclid's first four postulates still align well with our understanding of a two-dimensional metric space.
Euclid's fifth postulate, also known as the parallel postulate, was more troublesome. In Penrose words "it asserts that if two straight line segments [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] in a plane both intersect another straight line [math]\displaystyle{ c }[/math] (so that [math]\displaystyle{ c }[/math] is what is called a transversal of [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math]) such that the sum of the interior angles on the same side of [math]\displaystyle{ c }[/math] is less than two right angles, then [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math], when extended far enough on that side of [math]\displaystyle{ c }[/math], will intersect somewhere". One can see that the formulation of the fifth postulate is more complicated than the rest which lead to speculation of it's validity. With the fifth postulate one can go on to properly build a square and begin to explore the world of Euclidean geometry.
2.3 Similar-areas proof of the Pythagorean theorem[edit]
Penrose revisits the Pythagorean theorem by outlining another proof. Starting with a right triangle, subdivide the shape into two smaller triangles by drawing a line perpendicular to the hypotenuse through the right angle. The two smaller triangles are said to be similar to one another meaning they have the same shape but are different sizes. This is true because each of the smaller triangles has a right angle and shares an angle with the larger triangle. The third angle known because the sum of the angles in any triangle is always the same. Knowing that the sum of the area of the two small triangles equals the area of the big triangle (by construction), we can square the sides and show that the pythagorean theorem holds.
Again Penrose asks us to revisit our assumptions and examine which of Euclid's postulates were needed. Particularly our claim that the sum of the angles in a triangle add up to the same value of 180° (or [math]\displaystyle{ \pi }[/math] radians). One must use the parallel postulate to show that this is true. Penrose asks us to consider what would it mean for the parallel postulate to be false? What would that imply? Would that make any sense? With these questions in mind we begin to explore a different kind of geometry.
2.4 Hyperbolic geometry: conformal picture[edit]
The topic of questioning fundamental assumptions is taken to a level deeper with the example of Euclid’s fifth postulate and hyperbolic geometry, illustrated with M.C. Escher’s Circle limit I. The notion that all the black and white fish near the boundary are equal in ‘size’ to the fish near the center starts the section with an interesting point of confusion between our visual perception of Euclidean geometry and the hyperbolic representation.
Within the hyperbolic plane, Euclid’s first four postulates hold true, however, the fifth parallel postulate is false. Penrose notes some interesting consequences of this are that the interior angles of a triangle do not add to π, the Pythagorean theorem fails to hold, and a given shape does not have a similar shape of a larger size. The idea of conformal representations is then introduced with the example that angular relations between lines in the Euclidean and this representation of the hyperbolic plane are precisely the same.
Penrose then gives us the relation between the interior angles of the hyperbolic triangle to its area and says that while there is a sense of ‘unpleasantness’ with the fact that the sum of the interior angles of a triangle within the hyperbolic frame do not add to π, there is something ‘elegant and remarkable’ in direct relation of these angles to the area of the triangle, which is impossible to show within the Euclidean framework. He then leaves us with the equation for hyperbolic distance and notes that with this, hyperbolic geometry has all the properties of Euclidean geometry apart from those that need the parallel postulate, and this allows us to form congruent shapes.
2.5 Other representations of hyperbolic geometry[edit]
Since hyperbolic geometry is a more abstract construct, the conformal representation presented in section 2.4 is not the only way to represent hyperbolic geometry in terms of Euclidean geometry. Projective representations are next presented, where the difference is that hyperbolic straight lines are now represented as Euclidean straight lines. The cost of this ‘simplification’ is that angles are no longer the same. Penrose gives the reader an equation which allows the projective geometry to be obtained from a radial expansion from the center of the conformal representation.
The geometer Eugenio Beltrami is introduced as having discovered a geometric method relating these different hyperbolic representations which involve projections from the plane to spherical surfaces and back. Imagine the hyperbolic plane cuts a sphere at the equator. Hemispheric representation is the hyperbolic geometry representation on the northern hemisphere of the Beltrami sphere, found from projecting the projective representation upward onto its surface. Straight Euclidean lines in the plane are now semicircles which meet the equator orthogonally. Stereographic projection is introduced with the example of projecting these semicircles back onto the plane but projecting from the point of the south pole. This beautifully gives us the conformal representation on the plane. Two important properties of stereographic projection are:
- Conformal, so angles are preserved
- Sends circles on the sphere to circles on the plane
It is then emphasized that each of these representations are merely ‘Euclidean models’ of hyperbolic geometry and are not to be taken as what the geometry actually ‘is’. In fact, there are more representations such as the Minkowskian geometry of special relativity. The idea of a generalized ‘square’ is then presented in conformal and projective hyperbolic representations to show an interesting generalization of the Euclidean square.
2.6 Historical aspects of hyperbolic geometry[edit]
A historical backdrop is painted for the discovery of hyperbolic geometry as well as the importance of the proof by contradiction. Girolamo Saccheri’s work in 1733 used the proof by contradiction in attempt to prove Euclid’s fifth, but failed to show a contradiction. He did however discover the nature of hyperbolic geometry.
Following Saccheri, Heinrich Lambert derived many results by using this same method, including the hyperbolic angle/area relation that was mentioned in section 2.4. His tentative reasoning for belief in a consistent geometry without the fifth postulate was thinking about geometry on a ‘sphere of imaginary radius’. To illustrate this, Thomas Hariot’s angle/area relation for a Euclidean spherical triangle is given and compared to Lamberts hyperbolic relation. Lambert’s formula is recovered by replacing R2 with -1/R2 , showing that the ‘pseudo-radius’ is in fact imaginary: -C-1/2 .
Penrose makes the point that there are many instances in mathematics where the name attached to a concept is not that of the original discoverer. Some examples given:
- It is typical to attribute the discovery and first full acceptance of this geometry differing from Euclid’s via the absence of the fifth postulate to Carl Friedrich Gauss, but because Gauss did not publish his work, Janos Bolyai and Nicolai Ivanoivich Lobachevsky are also named as having independently rediscovered this geometry a few decades later. Hyperbolic geometry is frequently referred to as Lobachevskian geometry.
- Eugenio Beltrami was mentioned in section 2.5 for the discovery of the relations between the projective and conformal, via the hemispherical realizations. The conformal representation is commonly referred to as the Poincare model and the projective representation as the ‘Klein’ representation after their rediscoveries later in the 19th century. Beltrami is however best known for his pseudo-sphere representation involving Newton’s tractrix curve.
2.7 Relation to physical space[edit]
Penrose ends chapter 2 with a short discussion on the applicability of hyperbolic geometry to physical space. He notes that the geometry works perfectly well in higher dimensions and asks the question about our universe on cosmological scale. Is it Euclidean? Hyperbolic?
There are three types of geometry that would satisfy isotropy and homogeneity: Euclidean, hyperbolic, and elliptic. Einstein’s general relativity shows that Euclidean, although very accurate, is only an approximation of the actual geometry. We do not yet know the answer to the above question. There is evidence and support for each of the three geometries, but Penrose is transparent in his preference of the hyperbolic argument.
Penrose states that ‘fortunately for those…who are attracted to the beauties of hyperbolic geometry’, the space of velocities, according to modern relativity theory, is certainly a three-dimensional hyperbolic geometry rather than Euclidean.
He ends the chapter by stating that the Pythagorean theorem remains vital. The ‘Riemannian’ geometries that generalize hyperbolic geometry depend on the theorem in the limit of small distances, even though it is superseded for ‘large’ distances.
Chapter 3 Kinds of number in the physical world[edit]
3.1 A Pythagorean catastrophe?[edit]
We now switch over to the idea of ‘number’, and the layers of generality that lie beneath integers. The Pythagoreans solved the question, by using proof by contradiction, of attempting to find a rational number (fraction) whose square is precisely 2. There does not exist such a number within the confines are integers and rationals, which was troubling for them at the time since it was desired to have all of geometry be described by these types of physical numbers.
Penrose gives the proof by contradiction for the Pythagorean question above and explains the necessity of identifying the precise assumptions that go into a proof. He explains that there exist other generalities than that was originally used in the proof, whereby these precise assumptions must be used to judge the logic. The Pythagoreans used integers and rationals to explain the existence of the real numbers.
3.2 The real number system[edit]
Natural Numbers:
‘Counting’ numbers from 1 to [math]\displaystyle{ \infty }[/math].
Whole Numbers:
All counting numbers including 0, cannot be a fraction.
Integers:
All natural numbers and their negative counterparts and 0. If and are integers, then their sum , their difference , and their product are all integers (that is, the integers are closed under addition and multiplication), but their quotient may or may not be an integer, depending on whether can be divided by with no remainder.
Rational Numbers:
A number that can be expressed as the ratio a/b of two integers (or whole numbers) a and b, with b non-zero. The decimal expansion is alyas ultimately periodic, at a certain point the infinite sequence of digits consists of some finite sequence repeated indefinitely.
Irrational Numbers:
A number that cannot be expressed as the ratio of two integers. When an irrational number is expressed in decimal notation it never terminates nor repeats.
- Quadratic Irrational Numbers
- Arise in the solution of a general quadratic equation:
- [math]\displaystyle{ Ax^{2} + Bx + C = 0 }[/math]
- With A non-zero, the solutions being (derived from the quadratic formula):
- [math]\displaystyle{ -\frac{B}{2A}\sqrt{\left(\frac{B}{2A}\right)^2}+\frac{C}{A}, \quad -\frac{B}{2A}\sqrt{\left(\frac{B}{2A}\right)^2}-\frac{C}{A} }[/math]
- where, to keep within the realm of real numbers, be must have B2 greater than 4AC. When A, B, and C are integers or rational numbers, and where there is no rational solution to the equation, the solutions are quadratic irrationals.
Real Numbers:
A number in the set of all numbers above that falls on the real number line. It can have any value.
- Algebraic Real Numbers:
- Any number that is the solution to a polynomial with rational coefficients.
- Transcendental Real Numbers
- Any number that is not the solution to a polynomial with rational coefficients.
3.3 Real numbers in the physical world[edit]
Penrose states that while the historical driving force for mathematical ideas were to find constructs that mimic the behavior of the physical world, it is normally not possible to examine the physical world in such precise detail to abstract clear cut mathematics from it. Instead, the mathematics provides its own ‘momentum’ within the subject itself whereby it may seem to diverge from what it had been set up to achieve, but ultimately leads us to a deeper meaning of the world.
The real number system is given as an example of this since no direct evidence from Nature exists to show that the physical notion of ‘distance’ extends from arbitrarily large scales to the indefinitely tiny. Though, from cosmological scale to the quantum, to volumes and the metrics of spacetime, the ranges are increasing, and the fundamentals of calculus rely on the infinitesimal.
We may still ask whether the real number system is ‘correct’ for describing the physical universe or have we gotten lucky with extrapolation thus far. Penrose describes quantum mechanics as not implying any discreteness to Nature, nevertheless this idea may persist and echoes a quote from Einstein’s last published work where he suggested ‘discretely based algebraic theory’ might be the way forward for future physics. Penrose ends with stating that his idea of spin networks are both discrete and foundational in quantum gravity, led to his Twistor Theory, but real numbers are still fundamental in our understanding of the physical world.
3.4 Do natural numbers need the physical world?[edit]
Progressing this philosophical train of thought to the natural numbers, Penrose notes that the operations of addition and multiplication of natural numbers are independent of the nature of geometry of the world. Perhaps our notion of these numbers depends upon our universe specifically, but he stresses that it is hard to imagine that there would not be an important role for such fundamental entities.
To support this, Penrose introduces us to the idea of a set, which is an abstraction that does not appear to be tied to the specific structure of the universe. He then describes a method by which an empty or null set can be used to conjure the natural number system, out of nothing but the abstract idea of a set itself, and states that this technique can be used for the real number system as well.
Penrose ends by referring us back to Fig 1.3 (depiction of the mental, physical, and platonic worlds) and notes the mysterious nature of the fact that natural and real numbers having no reliance on the physical world for their existence, yet they seem to have direct relevance in describing the structure of the world.
3.5 Discrete numbers in the physical world[edit]
What might it mean to say that there are minus three cows in a field? An interesting question to start us thinking about the nature of discrete numbers and negatives in our world as defined as scalar quantities. Penrose states that only in the last hundred years that the integers in the negative seem to have direct physical relevance.
Electric charge is quantified in terms of integral multiples, positive, negative, or zero. Further, the three quarks within protons have charges 2/3, 2/3, -1/3. Is this the fundamental entity, and as such, the basic unit of charge is 1/3? This is just one example of an additive quantum number and Penrose notes that our present knowledge is that “all known additive quantum numbers are indeed quantified in terms of the system of integers…” Further, Dirac’s antiparticle theory shows us a physical and meaningful use for the negative numbers in which the additive quantum number of the antiparticle has precisely the negative of the value that it has for the original particle.
Penrose ends the chapter by stating that there are other kinds of number that appear to play a fundamental role in the universe, the most important and striking of which are the complex numbers. While they are fundamental to mathematics, “it is an even more striking instance of the convergence between mathematical ideas and the deeper workings of the physical universe”.
Chapter 4 Magical Complex Numbers[edit]
Penrose introduced the complex numbers, extending addition, subtraction, multiplication, and division of the reals to the system obtained by adjoining i, the square root of -1. Polynomial equations can be solved by complex numbers, this property is called algebraic closure and follows from the Fundamental Theorem of Algebra.
Complex numbers can be visualized graphically as a plane, where the horizontal coordinate gives the real coordinate of the number and the vertical coordinate gives the imaginary part. This helps understand the behavior of power series; for example, the power series [math]\displaystyle{ 1-x^2+x^4+\cdots }[/math] converges to the function [math]\displaystyle{ 1/(1+x²) }[/math] only when [math]\displaystyle{ |x|\lt 1 }[/math], despite the fact that the function doesn't seem to have "singular" behavior anywhere on the real line. This can be explained by switching to the complex number system using [math]\displaystyle{ z=x+iy }[/math] whereby [math]\displaystyle{ 1/(1+z²) }[/math] can be examined to have singularities at [math]\displaystyle{ x=i,-i }[/math].
With this, Penrose introduces us to the idea of the circle of convergence as a circle in the complex plane centered at 0 with poles/singularities of [math]\displaystyle{ f(z) }[/math] defining the circle radius. The series is convergent for any point z inside of this circle.
Finally, the Mandelbrot set is defined as the set of all points [math]\displaystyle{ c }[/math] in the complex plane so that repeated applications of the transformation mapping [math]\displaystyle{ z }[/math] to [math]\displaystyle{ z^2+c }[/math], starting with [math]\displaystyle{ z=0 }[/math], do not escape to infinity.
Chapter 5 Geometry of logarithms, powers, and roots[edit]
5.1 Geometry of complex algebra[edit]
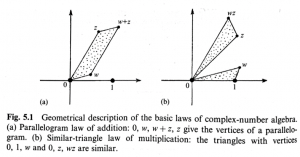
Penrose asks us to view complex addition and multiplication as transformations from the complex plane to itself, rather than just as simple addition and multiplication. The visual representations of these operations are given as the parallelogram and similar-triangle laws for addition and multiplication respectively.
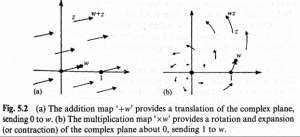
Rather than just ‘adding’ and ‘multiplying’ these can be viewed as ‘translation’ and ‘rotation’ within the complex plane. For example, multiply a real number by the complex number [math]\displaystyle{ i }[/math] rotates the point in the complex plane π/2 and viewing the parallelogram and similar-triangle laws as translation and rotation:
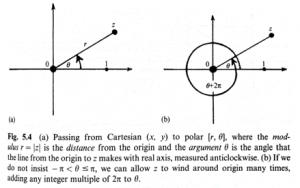
Penrose further introduces the concept of polar coordinates where [math]\displaystyle{ r }[/math] is the distance from the origin and [math]\displaystyle{ θ }[/math] is the angle made from the real axis in an anticlockwise direction.
5.2 The idea of the complex logarithm[edit]
Armed with both the cartesian and polar representations of complex numbers, it is now possible to show that the multiplication of two complex numbers leads to adding their arguments and multiplying the moduli. This, for the moduli, converts multiplication into addition.
This idea is fundamental in the use of logarithms. We first start with the expression [math]\displaystyle{ b^{m+n} = b^m \times b^n }[/math], which represents the idea of exponentiation. This is easy to grasp for [math]\displaystyle{ m }[/math] and [math]\displaystyle{ n }[/math] being positive integers, as each side just represents [math]\displaystyle{ m+n }[/math] instances of the number [math]\displaystyle{ b }[/math], all multiplied together. If [math]\displaystyle{ b }[/math] is positive, this law is then showed to hold for exponents that are positive integers, values of 0, negative, and fractions. If [math]\displaystyle{ b }[/math] is negative, we require further expansion into the complex plane.
We would need a definition of [math]\displaystyle{ b^p }[/math] for all complex numbers [math]\displaystyle{ p,q,b }[/math] such that [math]\displaystyle{ b^{p+q} = b^p \times b^q }[/math]. If we then define the logarithm to the base b as the inverse of the function [math]\displaystyle{ f(z) = b^z }[/math] such that [math]\displaystyle{ z=log_bw }[/math] for [math]\displaystyle{ w=b^z }[/math] then we should expect [math]\displaystyle{ z=log_b(p \times q) = log_bp + log_bq }[/math]. This would then convert multiplication into addition and allow for exponentiation in the complex plane.
5.3 Multiple valuedness, natural logarithms[edit]
We need to be careful with the above assertion of the logarithm, mainly since [math]\displaystyle{ b^z }[/math] and [math]\displaystyle{ log_bw }[/math] are ‘many valued’. Solving the equations would require a particular choice for [math]\displaystyle{ b }[/math] to isolate the solution. With this, the ‘base of natural logarithms’ is introduced as the number e, whose definition is the power series [math]\displaystyle{ 1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+… }[/math]. This power series converges for all values of z which then makes for an interesting choice to solve the ambiguity problem above. Thus we can rephrase the problem above with the natural logarithm, [math]\displaystyle{ z=logw }[/math] if [math]\displaystyle{ w=e^z }[/math].
However, even with this natural logarithm we run into multi-valuedness ambiguity from above. Namely that [math]\displaystyle{ z }[/math] still has many values that lead to the same solution with [math]\displaystyle{ z+2πin }[/math], where [math]\displaystyle{ n }[/math] is any integer we care to choose. This represents a full rotation of [math]\displaystyle{ 2π }[/math] in the complex plane with all multiples of [math]\displaystyle{ n }[/math] achieving the same point, [math]\displaystyle{ z }[/math].
Penrose goes further in representing [math]\displaystyle{ z }[/math] with polar coordinates showing [math]\displaystyle{ z=logr+iθ }[/math], then [math]\displaystyle{ e^z=re^{iθ} }[/math]. This formulation shows us that when we multiply two complex numbers, we take the product of their moduli and the sum of their arguments (using the addition to multiplication formula introduced in 5.2).
Rounding out the chapter, Penrose gives us another further representation of assuming [math]\displaystyle{ r=1 }[/math], such that we recover the ‘unit circle’ in the complex plane with [math]\displaystyle{ w=e^{iθ} }[/math]. We can 'encapsulate the essentials of trigonometry in the much simpler properties of complex exponential functions' on this circle by showing [math]\displaystyle{ e^{iθ}=cos(θ) + isin(θ) }[/math].
- [math]\displaystyle{ e^{i\theta} }[/math] is helpful notation for understanding rotating
- [math]\displaystyle{ e^{i\theta} = cos \theta + i sin \theta }[/math]
- (Worth looking into Taylor Series, which is related.)
5.4 Complex Powers[edit]
Returning to the ambiguity problem of multi-valuedness, it seems the best way to avoid issues is when a particular choice of [math]\displaystyle{ logw }[/math] has been specified. As an example, [math]\displaystyle{ w^z }[/math] with [math]\displaystyle{ z=\frac{1}{2} }[/math]. We can specify a rotation for [math]\displaystyle{ logw }[/math] to achieve [math]\displaystyle{ +w^\frac{1}{2} }[/math], then another rotation of [math]\displaystyle{ logw }[/math] to achieve [math]\displaystyle{ -w^\frac{1}{2} }[/math]. The sign change is achieved because of the Euler formula [math]\displaystyle{ e^{πi}=-1 }[/math]. Note the process: [math]\displaystyle{ w^z=e^{zlogw}=e^{zre^{iθ}}=e^{ze^{iθ}} }[/math], then specifying rotations for theta allows us to achieve either [math]\displaystyle{ +w^\frac{1}{2} }[/math] or [math]\displaystyle{ -w^\frac{1}{2} }[/math].
Penrose notes an interesting curiosity for the quantity [math]\displaystyle{ i^i }[/math]. We can specify [math]\displaystyle{ logi=\frac{1}{2}πi }[/math] because of the general relationship [math]\displaystyle{ logw=logr+iθ }[/math]. If [math]\displaystyle{ w=i }[/math], then its easy to see [math]\displaystyle{ logi=\frac{1}{2}πi }[/math] from noting that y is on the vertical axis in the complex plane (rotation of [math]\displaystyle{ \frac{π}{2} }[/math]). This specification, and all rotations, amazingly achieve real number values for [math]\displaystyle{ i^i }[/math].
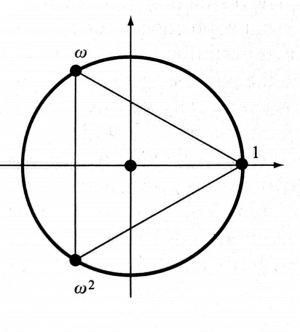
We end the section with the idea of finite multiplicative groups, or cyclic groups Zn, which contain [math]\displaystyle{ n }[/math] quantities (nth roots of unity if around the unit circle) with the property that any two can be multiplied together to get another member of the group. As an example, Penrose gives us [math]\displaystyle{ w^z=e^{ze^{i(θ+2πin)}} }[/math] with [math]\displaystyle{ n=3 }[/math], leading to three elements [math]\displaystyle{ 1, ω, ω^2 }[/math] with [math]\displaystyle{ ω=e^\frac{2πi}{3} }[/math]. Note [math]\displaystyle{ ω^3=1 }[/math] and [math]\displaystyle{ ω^-1=ω^2 }[/math]. These form a cyclic group Z3 and in the complex plane, represent vertices of an equilateral triangle. Multiplication by ω rotates the triangle through [math]\displaystyle{ \frac{2}{3}π }[/math] anticlockwise and multiplication by [math]\displaystyle{ ω^2 }[/math] turns it through [math]\displaystyle{ \frac{2}{3}π }[/math] clockwise. The cyclic group is graphically shown below:
5.5 Some Relations To Modern Particle Physics[edit]
Penrose rounds out the chapter with some examples of complex concepts in the world of particle physics. Additive quantum numbers were briefly introduced in section 3.5, and here we are introduced to multiplicative quantum numbers, which are quantified in terms of nth roots of unity.
The notion of parity is introduced as approximately a multiplicative quantum number with n=2, and an example is the family of particles called bosons. Penrose notes that fermions could also be considered a parity group but it is not the normal convention. The distinction between these two particles are that bosons are completely restored to their original states under a [math]\displaystyle{ 2π }[/math] rotation, whereas fermions require [math]\displaystyle{ 4π }[/math] (two rotations). Thus a multiplicative quantum number of [math]\displaystyle{ -1 }[/math] can be assigned to a fermion and [math]\displaystyle{ +1 }[/math] to a boson.
An example of a multiplicative quantum number with [math]\displaystyle{ n=3 }[/math] relates to quarks, which have values for electric charge that are not integer multiples of the electron’s charge, but in fact [math]\displaystyle{ \frac{1}{3} }[/math] multiples. If [math]\displaystyle{ q }[/math] is the value of electric charge with respect to an electron ([math]\displaystyle{ q=-1 }[/math] for electron charge), then quarks have q=[math]\displaystyle{ \frac{2}{3} }[/math] or [math]\displaystyle{ -\frac{1}{3} }[/math] and antiquarks q=[math]\displaystyle{ \frac{1}{3} }[/math] or [math]\displaystyle{ -\frac{2}{3} }[/math]. If we take the multiplicative quantum number [math]\displaystyle{ e^{-2qπi} }[/math], then we find the values [math]\displaystyle{ 1,ω,ω^2 }[/math] from section 5p4, which constitute the cyclic group Z3.
Chapter 6 Real-number calculus[edit]
6.1 What makes an honest function?[edit]
Calculus is built from the two ingredients, differentiation and integration. Differentiation is a local phenomenon which concerns the rates that things change whereby integration is a more quantity that measures the totality. Incredibly, these two ingredients are the inverse of one another (fundamental theorem of calculus).
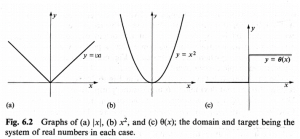
These two operate on ‘functions’ and Penrose notes that these can be thought of as ‘mappings’ from some array of numbers (domain) to another (target). Penrose gives the three examples below which will be used later in the chapter as mapping the real number system to itself:
6.2 Slopes of functions[edit]
Differentiation is concerned with and calculates the rates that things change, or ‘slopes’ of these things. For the curves given in section 6p1 above, two of the three do not have unique slopes at the origin and are said to be not differentiable at the origin, or not smooth there. Further, the curve of theta(x) has a jump at the origin which is to say that it is discontinuous there, whereas [math]\displaystyle{ |x| }[/math] and [math]\displaystyle{ x^2 }[/math] were continuous everywhere.
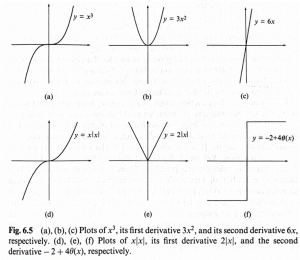
Taking differentiation a step further, Penrose shows us two plots which look very similar, but are represented by different functions, [math]\displaystyle{ x^3 }[/math] and [math]\displaystyle{ x|x| }[/math]. Each are differentiable and continuous, but the difference has to do with the curvature (second derivative) at the origin. [math]\displaystyle{ x|x| }[/math] does not have a well-defined curvature here and is said to not be twice differentiable.
6.3 Higher derivatives; [math]\displaystyle{ C^\infty }[/math]-smooth functions[edit]
Looking closer at the concept of two derivatives of the same function (second derivative, or curvature), Penrose shows us the functions from 6p2 and their first and second derivatives. Note that the first derivative of [math]\displaystyle{ f(x) }[/math], written [math]\displaystyle{ f’(x) }[/math], meets the x-axis at places of local minima or maxima and the second derivative of [math]\displaystyle{ f(x) }[/math], written [math]\displaystyle{ f’’(x) }[/math], meets the x-axis where the curvature goes to [math]\displaystyle{ 0 }[/math] and is said to be a point of inflection.
In general, a function can be smooth for many derivatives and the mathematical terminology for general smoothness is to say that [math]\displaystyle{ f(x) }[/math] is [math]\displaystyle{ C^n }[/math]-smooth. It can be seen that [math]\displaystyle{ x|x| }[/math] is [math]\displaystyle{ C^1 }[/math]-smooth but not [math]\displaystyle{ C^2 }[/math]-smooth due to the discontinuity at the origin in the derivative. In general [math]\displaystyle{ x^n|x| }[/math] is [math]\displaystyle{ C^n }[/math]-smooth but not [math]\displaystyle{ C^{n+1} }[/math]-smooth. In fact, a function can be [math]\displaystyle{ C^\infty }[/math]-smooth if it is smooth for every positive integer. Note that negative integers for [math]\displaystyle{ x^n }[/math] immediately are not smooth for [math]\displaystyle{ x^{-1} }[/math] (discontinuous at the origin).
Penrose notes that Euler would have required [math]\displaystyle{ C^\infty }[/math]-smooth functions to be defined as functions, and then gives the function:
- [math]\displaystyle{ h(x) = \begin{cases} 0, & \mbox{if } x \le 0 \\ e^{-\frac{1}{x}}, & \mbox{if } x \gt 0 \end{cases} }[/math]
as an example of a [math]\displaystyle{ C^\infty }[/math]-smooth function but one that Euler would still not be happy with since it is two functions stuck together.
6.4 The "Eulerian" notion of a function?[edit]
How, then do we define the notion of a ‘Eulerian’ function? This can be accomplished in two ways. The first using complex numbers and is incredibly simple. If we extend [math]\displaystyle{ f(x) }[/math] to [math]\displaystyle{ f(z) }[/math] in the complex plane, then all we require is for [math]\displaystyle{ f(z) }[/math] to be once differentiable (a kind of [math]\displaystyle{ C^1 }[/math]-smooth function). That’s it, magically. We will see that this can be stated with [math]\displaystyle{ f(x) }[/math] being an analytic function.
The second method involves power series manipulations, and Penrose notes that ‘the fact that complex differentiability turns out to be equivalent to power series expansions is one of the truly great pieces of complex-number magic’.
For the second method, the power series of [math]\displaystyle{ f(x) }[/math] is introduced, [math]\displaystyle{ f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + … }[/math] For this series to exist then it must be [math]\displaystyle{ C^\infty }[/math]-smooth. We must take and evaluate derivatives [math]\displaystyle{ f(x) }[/math] to find the coefficients, thus an infinite number of derivatives (positive integers) must exist for the power series to exist. If we evaluate [math]\displaystyle{ f(x) }[/math] at the origin, we call this a power series expansion about the origin. About any other point [math]\displaystyle{ p }[/math] would be considered a power series expansion about [math]\displaystyle{ p }[/math]. (Maclaurin Series about origin, see also Taylor Series for the general case)
The power series is considered analytic if it encompasses the power series about point [math]\displaystyle{ p }[/math]. If it is analytic at all points of its domain, we call it an analytic function or, equivalently, a [math]\displaystyle{ C^ω }[/math]-smooth function. Euler would be pleased with this notion of an analytic function, which is ‘smoothier’ than the set of [math]\displaystyle{ C^\infty }[/math]-smooth functions ([math]\displaystyle{ h(x) }[/math] from 6p3 is [math]\displaystyle{ C^\infty }[/math]-smooth but not [math]\displaystyle{ C^ω }[/math]-smooth).
- Physics in trying to understand reality by approximating it.
6.5 The rules of differentiation[edit]
- Armed with these few rules (and loads and loads of practice), one can become an "expert at differentiation" without needing to have much in the way of actual understanding of why the rules work!
6.6 Integration[edit]
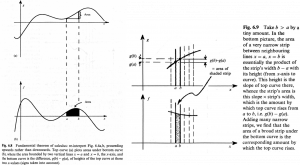
As stated in section 6p1, integration is the inverse of differentiation as stated in the fundamental theorem of calculus. Penrose provides the following visual and explanation. If we start with the differentiated curve, the area underneath the derivative curve bounded by two points on the x-axis, and the x-axis itself is equal to the difference in heights of the original curve evaluated at the two points.
Integration is noted as making the function smoother and smoother, whereas differentiation continues to make things ‘worse’ until some functions reach a discontinuity and become ‘non-differentiable’.
Penrose ends the chapter noting that there are approaches which enable the process of differentiation to be continued indefinitely, even if the function is not differentiable. One example is the Dirac Delta Function which is of ‘considerable importance in quantum mechanics’. This extends our notion of [math]\displaystyle{ C^n }[/math]-functions into the negative integer space ([math]\displaystyle{ C^{-1},C^{-2},... }[/math]) and will be discussed later with complex numbers. Penrose notes that this leads us further away from the ‘Eulerian’ functions, but complex numbers provide us with an irony that expresses one of their finest magical feats of all.
- If we integrated then differentiate, we get the same answer back. Non-commutative the other way.
Chapter 7 Complex-number calculus[edit]
7.1 Complex smoothness; holomorphic functions[edit]
An outline for section 7 is presented, in which calculus with complex numbers is introduced. The material in this chapter leads up to the explanation of holomorphic functions, which play a vital role in much of the mathematical as well as physics material later in the book.
To do so, the notion of a special type of integration along a contour in the complex plane is to be defined. This integration can then be used to solve for the coefficients of a Taylor series expression which allow for us to see that any complex function which is complex-smooth in the complex plane is necessarily analytic, or holomorphic.
As will be stated in 7.3, instead of directly providing the definition of holomorphic functions, Penrose chooses to demonstrate the argument with the ingredients in order to show a "wonderful example of the way that mathematicians can often obtain their results. Neither the premise ([math]\displaystyle{ f(z) }[/math] is complex-smooth) nor the conclusion ([math]\displaystyle{ f(z) }[/math] is analytic) contains a hint of the notion of contour integration or the multivaluedness of a complex logarithm. Yet these ingredients provide the essential clues to the true route to finding the answer".
7.2 Contour integration[edit]
In the real number sense, integrals are taken from a single point [math]\displaystyle{ a }[/math] to another point [math]\displaystyle{ b }[/math] along the real number line. Usually the horizontal axis, and there is only one way to travel along this line (moving positive and negative along the axis). However, in the complex plane points involve two dimensions, and therefore have many such routes that allow us to get from a complex point [math]\displaystyle{ a }[/math] to [math]\displaystyle{ b }[/math].
The Cauchy-Riemann equations (to be formally introduced later in chapter 10) allow us to narrow our focus to find a path-specific answer, where the value of the integral on this path is the same for any other path that can be formed from the first by continuous deformation in its domain. Note that the function [math]\displaystyle{ \frac{1}{z} }[/math] has a hole in the domain at the origin, which can prevent a continuous deformation thereby allowing for different answers for the value of the integral depending on the path taken.
Continuous deformation in this sense is defined as homologous deformation, where parts of the path can cancel each other out if they are traversed in opposite directions. This contrasts with homotopic paths where you may not cancel parts. As a visualization we take the function of [math]\displaystyle{ \frac{1}{z} }[/math] with a homologous path:
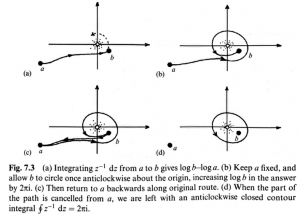
The amazing result here is that a general contour from [math]\displaystyle{ a }[/math] to [math]\displaystyle{ b }[/math] for the function [math]\displaystyle{ \frac{1}{z} }[/math] has be rephrased and shown to be equal to the result for a closed contour that loops around the point of non-analyticity (the origin in this case), regardless of where the points [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] (or the point of non-analyticity) lie in the complex plane. Note that since [math]\displaystyle{ logz }[/math] is multi-valued, we need to specify the actual closed contour being used (if we looped twice rather than once, then the answer is different).
7.3 Power series from complex smoothness[edit]
The example in section 7p2 is a particular case for the well-known Cauchy Integral Formula, which allows us to know what the function is doing at the origin (or another general point [math]\displaystyle{ p }[/math]) by what it is doing at a set of points surrounding the origin or the general point [math]\displaystyle{ p }[/math].
- [math]\displaystyle{ \frac{1}{2πi}\oint\frac{f(z)}{z-p}dz=f(p) }[/math]
A 'higher-order' version of this formula allows us to inspect [math]\displaystyle{ n }[/math] number of derivatives with the same relationship.
- [math]\displaystyle{ \frac{n!}{2πi}\oint\frac{f(z)}{(z-p)^{n+1}}dz=f^{(n)}(p) }[/math]
If we use this to provide the definition of a derivative at a point, we can then construct a Maclaurin formula (if using the origin, otherwise the more general Taylor series) for [math]\displaystyle{ f(z) }[/math] using the derivatives in the coefficients of the terms.
- [math]\displaystyle{ \sum_{n=0} ^ {\infty} \frac {f^{(n)}(p)}{n!} (z-p)^{n} }[/math]
This can be shown to sum to [math]\displaystyle{ f(z) }[/math], thereby showing the function has an actual [math]\displaystyle{ n }[/math]th derivative at the origin or general point [math]\displaystyle{ p }[/math]. This concludes the argument showing that complex smoothness in a region surrounding the origin or point implies that the function is also holomorphic. Penrose notes that neither the premise ([math]\displaystyle{ f(z) }[/math] is complex-smooth) nor the conclusion ([math]\displaystyle{ f(z) }[/math] is analytic) contains contour integration or multivaluedness of a complex logarithm, yet these ingredients are essential for finding the route to the answer and that this is a ‘wonderful example of the way that mathematicians can often obtain their results’.
7.4 Analytic continuation[edit]
We now know that complex smoothness throughout a region is equivalent to the existence of a power series expansion about any point in the region. A region here is defined as a open region, where the boundary is not included in the domain.
For example, if there is no singularity in the function, the region can be thought of as a circle of infinite radius. Taking [math]\displaystyle{ f(z)=\frac{1}{z} }[/math] however forces an infinite number of circles centered at any point with boundary radii passing through the origin (noting that an open region does not contain the boundary) to construct the domain.
Now we consider the question, given a function [math]\displaystyle{ f(z) }[/math] holomorphic in domain [math]\displaystyle{ D }[/math], can we extend the domain to a larger [math]\displaystyle{ D’ }[/math] so that [math]\displaystyle{ f(z) }[/math] also extends holomorphically? A procedure is formed in which we use a succession of power series about a sequence of points, forming a path where the circles of convergence overlap. This then results in a function that is uniquely determined by the values in the initial region as well as the path along which it was continued. Penrose notes this analytic continuation as a remarkable ‘rigidity’ about holomorphic functions.
An example of this rigidity and path dependence is ‘our old friend’ [math]\displaystyle{ logz }[/math]. There is no power series expansion about the origin due to the singularity there but depending on the path chosen of points around the origin (clockwise or anti-clockwise) the function extends or subtracts in value by [math]\displaystyle{ 2πi }[/math]. See chapter 5 and the euler formula ([math]\displaystyle{ e^{πi}=-1 }[/math]) for a refresher.