Graph, Wall, Tome: Difference between revisions
m (→Background) |
|||
| Line 14: | Line 14: | ||
[[File:sheetsunx.gif||Curved Space-Time]] | [[File:sheetsunx.gif||Curved Space-Time]] | ||
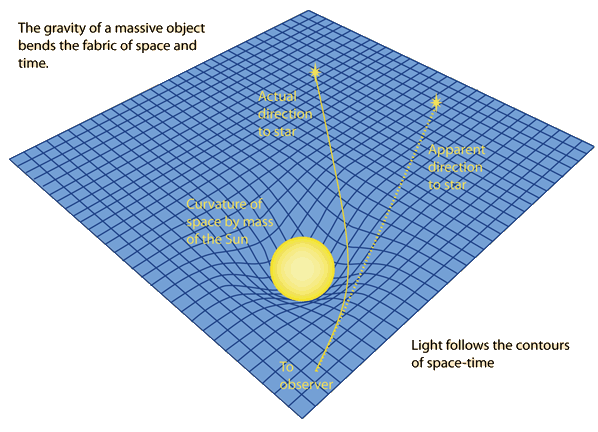
Instantly, the meaning becomes clear. Gravity warps space(time), and matter, planets, and even light follows a path | Instantly, the meaning becomes clear. Gravity warps space(time), and matter, planets, and even light follows a path that is curved by the warped geometry. | ||
Fundamental physics is an unknown world to most people. Equations, symbols, and incomprehensible terms abound, and unless you've studied post-grad mathematics and physics, this world is inaccessible to you. | Fundamental physics is an unknown world to most people. Equations, symbols, and incomprehensible terms abound, and unless you've studied post-grad mathematics and physics, this world is inaccessible to you. | ||
Revision as of 08:38, 30 January 2020
Background
Imagine: It's 1915, and you've made one of the greatest discoveries in hundreds of years. You visit your mother and show her your work:
$$R_{\mu v}-\frac{1}{2}Rg_{\mu v} = 8 \pi T_{\mu v}$$
'That's nice dear', she responds, unaware of the implications of your discovery.
The problem, is that although this equation carries with it the secrets of gravity, to a layman it is merely a bunch of letters.
Now, consider this single image.
Instantly, the meaning becomes clear. Gravity warps space(time), and matter, planets, and even light follows a path that is curved by the warped geometry.
Fundamental physics is an unknown world to most people. Equations, symbols, and incomprehensible terms abound, and unless you've studied post-grad mathematics and physics, this world is inaccessible to you.
Although there are several great resources to map the way toward complete understanding. Most people will not undertake the journey to understand the source code to the world that we all inhabit.
The GWT Project
Bringing an understanding of fundamental physics is one aim of The Portal.
There currently exist 3 resources that themselves contain all that you need for an almost complete understanding of the world.
- The Graph - A paragraph written by Ed Witten
- The Wall - The iconic wall of Stony Brook University
- The Tome - The book 'The Road to Reality' by Roger Penrose
These resources are available to everyone, but will be sought by almost none. The aim of the GWT project to convert these resources into a medium that can be widely disseminated, and which can not be ignored.
This project will require bi-directional information transfer, and the minds of people with many different aptitudes.
- We need mathematicians, topologists, geometers, and physicists to understand these resources, and all of their implications.
- We need explainers, and educators, to convey this information to a wider audience.
- And we need artists, linguists, and programmers to create intuitive visualisations.
The Portal will create a community of people, working together to that achieve these aims.
Success will generate yet further insights, perhaps opening up a more fundamental understanding of the nature of reality.
This was first collected in a Google Doc titled Graph, Wall, Tome - Problem Solving.
The Graph
If one wants to summarise our knowledge of physics in the briefest possible terms, there are three really fundamental observations:
- Spacetime is a pseudo-Riemannian manifold M, endowed with a metric tensor and governed by geometrical laws.
- Over M is a principal bundle $$P_{G}$$ with a non-abelian structure group G.
- Fermions are sections of $$(\hat{S}_{+} \otimes V_{R}) \oplus (\hat{S}\_ \otimes V_{\bar{R}})$$. $$R$$ and $$\bar{R}$$ are not isomorphic; their failure to be isomorphic explains why the light fermions are light.
- Add something about Higgs
All of this must be supplemented with the understanding that the geometrical laws obeyed by the metric tensor, the gauge fields, and the fermions are to be interpreted in quantum mechanical terms.
Origin
This is a modified version of the paragraph by Edward Witten as posted by Eric via Twitter.
Eric Weinstein suggested several alterations, that have been included above:
- In (ii), “vector bundle X” should be changed to principal G-bundle.
- Also in (ii), “nonabelian gauge group G” should be changed to nonabelian structure group G.
- In (iii), [math]\displaystyle{ \ R }[/math] and [math]\displaystyle{ \tilde R }[/math] should be (complex) linear representations of G and so they are not equivalent.
The Wall
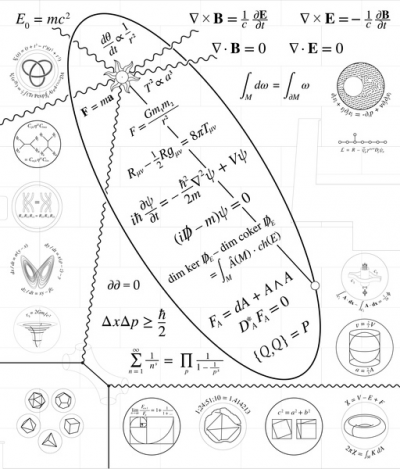
This image is carved into a wall at Stony Brook University. It contains many of the most fundamental equations of physics, providing a formulaic representation of all reality.
Several of the equations have been identified as having direct connections to statements in 'The Graph' (identified by numbers)
Equations
1: Einstein's General Relativity equation:
- $$R_{\mu v}-\frac{1}{2}Rg_{\mu v} = 8 \pi T_{\mu v}$$
2: Maxwell's equations:
- $$\nabla \times \mathbf{B} = \frac{1}{c} \frac{\partial \mathbf{E}}{\partial t}$$
- $$\nabla \times \mathbf{E} = -\frac{1}{c} \frac{\partial \mathbf{B}}{\partial t}$$
- $$\nabla \cdot \mathbf{B} = 0$$
- $$\nabla \cdot \mathbf{E} = 0$$
2: Yang-Mills equations:
- $$d^*_A F_A \propto J$$
3: Dirac equation:
- $$(i \not{D}_A - m)\psi = 0$$
4: Klein-Gordon equation: (this is not included in 'The Wall', but it has been suggested that perhaps it should have been)
- $$\frac{1}{c^2} \frac{\partial^2}{\partial t^2} \psi - \nabla^2 \psi + \frac{m^2 c^2}{\hbar^2} \psi = 0$$
Einstein's mass-energy equation:
- $$E = mc^2$$
Kepler's 2nd law:
- $$\frac{d\theta}{dt} \propto \frac{1}{r^2}$$
Newton's force-acceleration equation:
- $$\mathbf{F} = m\mathbf{a}$$
Keplers 3rd law:
- $$T^2 \propto a^3$$
Newtons gravitational law:
- $$F = \frac{G m_1 m_2}{r^2}$$
Schrodinger's equation:
- $$i \hbar \frac{\partial \psi}{\partial t} = - \frac{\hbar^2)}{2 m} \nabla^2 \psi + V \psi$$
Atiyah-Singer theorem:
- $$dim\, ker \not{D}_E - dim \, coker \not{D}_E = \int_M \hat{A}(M) \cdot ch(E)$$
Defining relation of supersymmetry:
- $$\{Q,Q\} = P$$
Stokes' theorem:
- $$\int_M d\omega = \int_{\partial M}\omega$$
The boundary of a boundary is zero:
- $$\partial\partial = 0$$
Heisenberg's indeterminacy relation:
- $$\Delta x \Delta p \geq \frac{\hbar}{2}$$
Euler's formula for Zeta-function:
- $$\sum\limits_{n=1}^{\infty} \frac{1}{n^{s}} = \prod\limits_{p} \frac{1}{1 - \frac{1}{p^s}}$$
Eric talked about some of the important equations on the wall. There are 2 different recorded versions of the conversation if you want to listen to it.
The Tome
This book by Roger Penrose constains a comprehensive account of the physical universe.
To gain an understanding and intuition for the information contained in 'The Graph', and 'The Wall', reading this book will provide a great head-start.
With 34 chapters spread over 1000 pages, including diagrams, equations, and descriptions, there is are multiple avenues for understanding all concepts.
Book Details
- ISBN: 978-0679776314
- Road to Reality by Roger Penrose (2004)
- There appears to be a Kindle Edition that isn't available in the US. If anyone in the community has a way to get a Kindle version of the book, please add it here.
- Purchase the book somehow, then get the pdf here
Questions
Some questions Eric posed related to the assignment:
What is $$F_A$$ geometrically?
What are $$R_{\mu v}$$ and $$R$$ geometrically?
Einstein field equaitions Einstein’s original publication, Die Feldgleichungen der Gravitation, in English
$$R$$
$$R$$ is a scalar value, describing the "curvature of the spacetime manifold" at each point along the manifold. It's based on a concept of 'parallel transport', where you move a vector around some path on the manifold.
$$R$$ can be computed at each point on the manifold, and describes the difference in the vector's angle after following an infinitesimally small path around the neighborhood of that point, vs. what it was originally. The video does a great job of visualizing when and why that vector angle change would happen, with flat vs. curved manifolds.
In the video, they focus first on the curvature of space. Hopefully they incorporate back in curvature in time, because that's less obvious.
$$R_{\mu v}$$
The same video then proceeds to explain $$R_{\mu v}$$. It progresses through some concepts.
Computing length in non-orthogonal bases
First, just describing the length of a vector on a curved space is hard. It is given by:
$$Length^{squared} = g_{11}dX^{1}dX^{1} + g_{12}dX^{1}dX^{2} + g_{21}dX^{2}dX^{1} + g_{22}dX^{2}dX^{2}$$
Some notes:
- This is not Pythagorean theorem, because $$dX^{1}$$ and $$dX^{2}$$ are not perpendicular.
- Instead, looks like a formula to get the diagonal from two opposite vertices in a parallelogram.
- If $$dX^{1}$$ and $$dX^{2}$$ are perpendicular, then $$g_{12}$$ and $$g_{21}$$ would be 0, and we would get $$Length^{squared} = g_{11}(dX^{1})^{2} + g_{22}(dX^{2})^{2}$$
- See: the video @ 14m27s
Computing vector rotation due to parallel transport
Then, they show parallel transport when following a parallelogram, but over a curved 3D manifold. To compute the vector rotation by components, they show:
$$dV^{1} = dX^{1}dX^{2} (V^{1}R^{1}_{112} + V^{2}R^{1}_{212} + V^{3}R^{1}_{312})$$
$$dV^{2} = dX^{1}dX^{2} (V^{1}R^{2}_{112} + V^{2}R^{2}_{212} + V^{3}R^{2}_{312})$$
$$dV^{3} = dX^{1}dX^{2} (V^{1}R^{3}_{112} + V^{2}R^{3}_{212} + V^{3}R^{3}_{312})$$
or, using $$i$$ to summarize across all 3 components (difference vectors):
$$dV^{i} = dX^{1}dX^{2} (V^{1}R^{i}_{112} + V^{2}R^{i}_{212} + V^{3}R^{i}_{312})$$
or , using $$j$$ to index over all 3 components (original vector):
$$dV^{i} = dX^{1}dX^{2} \Sigma_{j} [(V^{j}R^{i}_{j12}]$$
See: the video @ 19m33s
Open questions:
- Why a parallelogram?
- How to properly overlay the parallelogram onto the 3d manifold, in order to do the parallel transport?
- How does this relate to the length computation above?
Putting it all together
Now, moving to 4D, we can compute $$R_{\mu v}$$ as:
$$R_{00} = R^{0}_{000} + R^{1}_{010} + R^{2}_{020} + R^{3}_{030}$$
$$R_{10} = R^{0}_{100} + R^{1}_{110} + R^{2}_{120} + R^{3}_{130}$$
$$R_{01} = R^{0}_{001} + R^{1}_{011} + R^{2}_{021} + R^{3}_{030}$$
etc.
Indexing i over all 4 component vectors / dimensions, we get:
$$R_{00} = \Sigma_{i} R^{i}_{0i0}$$
$$R_{10} = \Sigma_{i} R^{i}_{1i0}$$
$$R_{01} = \Sigma_{i} R^{i}_{0i1}$$
etc.
Summarizing on $$\mu$$, we get:
$$R_{\mu 0} = \Sigma_{i} R^{i}_{\mu i0}$$
$$R_{\mu 1} = \Sigma_{i} R^{i}_{\mu i1}$$
etc
Summarizing on $$v$$, we get:
$$R_{\mu v} = \Sigma_{i} R^{i}_{\mu iv}$$
Open questions:
- If we hadn't moved from 3D to 4D, what would this all have looked like?
- What does this have to do with the parallelogram?
- Why are there two indices?
How do they relate?
What does this have to do with Penrose Stairs?
We’ve heard Eric talk about Penrose stairs and spinors - essentially phenomena where you cannot return to the original state through a 360 degree rotation, but require a 720 degree rotation.
What are “Horizontal Subspaces” and what do they have to do with Vector Potentials or Gauge fields?
From theplebistocrat:
Generally, we're wanting to understand how fermions arise from - or are embedded within / upon - topological "spaces" that have distinct rules which govern operations within those topological spaces, and then how those rules produce higher dimensional operations in corresponding spaces.
Just intuitively, and geometrically speaking, the image that I'm getting when describing all of this and trying to hold it in my head is the image of a sort of Penrose Tower of Babel, where the fundamental underlying structures reach upwards (but also downwards and inwards?) before reaching a critical rotation that corresponds to a collapse of structure into a higher dimensional fiber bundle.
But doesn't this require the symmetry break? How is left and right rotation in a subspace transformed into verticality? This is a crazy rabbit hole, friends. Keep your chins up. Let me know if this was helpful or leading astray.