20: Sir Roger Penrose - Plotting the Twist of Einstein’s Legacy
Description
Roger Penrose is arguably the most important living descendant of Albert Einstein’s school of geometric physics. In this episode of The Portal, we avoid the usual questions put to Roger about quantum foundations and quantum consciousness. Instead we go back to ask about the current status of his thinking on what would have been called “Unified Field Theory” before it fell out of fashion a couple of generations ago. In particular, Roger is the dean of one of the only rival schools of thought to have survived the “String Theory wars” of the 1980s-2000s. We discuss his view of this Twistor Theory and its prospects for unification. Instead of spoon feeding the audience, however, the material is presented as it might occur between colleagues in neighboring fields so that the Portal audience might glimpse something closer to scientific communication rather than made for TV performance pedagogy. We hope you enjoy our conversation with Prof. Penrose.
Participants
- Eric Weinstein (WEIN)
- Roger Penrose (PEN)
Housekeeping
WEIN - Hello, this is Eric. 2 pieces of housekeeping:
- On Bret and Heather (we will resume that thread when they return from the jungle)
- On today’s guest. Eric mentions;
- The Emperor’s New Mind
- Many Worlds
- Quantum Entanglement
- Penrose’s early work, for example with Hawking (eg; [Penrose-Hawking Singularity Theorems]).
1:00 = Roger is famous for being one of the greatest Geometric Physicists now living and perhaps the best descendent of Albert Einstein currently still working in Theoretical Physics in this particular line of thought. Also, he is an example of what the UK does well.
1:30 = …if you start to feel as though you are being left behind by one line of thinking, what we do in general is wait to see if a different line of thinking opens up… …this is normal.
2:30 = welcome Roger
3:00 = WEIN - “I know you as one of the most important people at the nexus of Geometry and Physics”
Lyrics from the Leonard Cohen song, “The Future” (“You don’t know me from the wind, you never will, you never did, but I’m the little jew who wrote the bible”)
Book: The Road to Reality, by Roger Penrose (this appears to be easily accessible online as a pdf)
4:00 = WEIN - “Where are we in the history of coming to understand what this place is in which we find ourselves? What we are made of? And what we know about our own context?”
PEN - “I now feel I should re-write part of it (the Road to Reality) because since I wrote it things have changed in one important way” *
<<<Did he say what the one way it had changed was?
PEN - “A lot has not changed - the thing that has changed… …is to do with Cosmology.”
PEN - I have a proposal… which is new since I wrote that book
[NOTE: I’m not sure if he ever gets back to saying what this proposal is. It looks like it might be “Conformal Cyclic Cosmology”, see eg; Physics World, ibid, his own book, Cycles of Time]
6:00 =
Penrose brief biography.
Penrose;
- Born ‘31.
- Took classes from Paul Dirac
- Was undergraduate at UCL
- Went to Cambridge for graduate studies.
- Went to study Algebraic Geometry, not Physics
PEN - “I’d encountered a friend of my brothers, Dennis Sciama.” * (see also the note below)
<<<This name took some finding
Sciama gave lectures on Cosmology and talked about steady state theories in which the Universe expands but doesn’t change because it’s continually ‘replenished’ by the creation of new matter.
Penrose’s older brother, Oliver Penrose who was studying Statistical Mechanics was the precocious one (of the two brothers).
Penrose had also been listening to talks byFred Hoyle who suggested that when the matter in the accelerating expansion reaches the speed of light it disappears.
Penrose didn’t think that was quite right and started drawing pictures with Light Cones and thought they would gradually fade, but not disappear.
8:00 = Talking to his brother in the Kingswood Restaurant, Cambridge *, Roger expressed his doubts and was referred to Dennis.
[NOTE: I tried to find a link for this restaurant, which appears to no longer exist, and came across this really interesting paper by Professor Penrose and George Ellis, which is a kind of “scientific eulogy”* for Dennis Sciama, in which the same anecdote is recalled, amongst others: https://royalsocietypublishing.org/doi/pdf/10.1098/rsbm.2009.0023 (pdf) ]
<<<There’s probably a better term for this, right?
<<<When I search for ‘“the kingswood restaurant” cambridge’ I don’t turn up anything that seems relevant and when I add the word “remember” to that search I start to turn up links to Sir Roger himself.Possibly it was called by a different name. Also possible that no trace of it has made it onto the internet other than his telling.
Dennis Sciama was impressed! Later, when Roger came up, he took him under his wing.
Penrose’s supervisor was Hodge - W.V.D Hodge
But later he threw Roger out and Todd became his supervisor - J.A Todd *
<<<The links I’ve added to Hodge and Todd both seem right but I’m not personally familiar
Ad Break
9:00 = advert for a watches. Masculinity, something, something….
10:00 = advert for lamps. Mention of the Matrimandir (looks nice, might buy a lamp)
Dennis Sciama
11:00 = Dennis wanted Roger to be a Cosmologist
Dennis had a knack of making sure people met each other. In one case it was Stephen Hawking
Dennis was the last (at the time the only) graduate student of Paul Dirac.
Book: The Strangest Man: The Hidden Life of Paul Dirac, Mystic of the Atom by Graham Farmelo
PEN - Dirac was hard to get to know.
WEIN - Dirac would be neck and neck with Einstein for greatest 20th Century Physicist.
Eric imputes that Dirac’s hair was not as good as Einstein’s.
PEN - Dirac was the one who put QM in order
Taste and Beauty
The Hopf Fibration (source,gif)
WEIN - “you have wielded taste and beauty as a weapon your entire life, your drawings are among the most compelling”
13:00 = “Our friend Joe Rogan” *
Joe Rogan * is a prominent Podcaster and Cage-fighting Commentator
<<<Roger Penrose and Eric Weinstein are friends with the guy who does the commentary for the cage fighting. It’s quite a time to be alive.
<<<If you have ever been on Joe Rogan’s Podcast and now have your own podcast, you are contractually obliged to mention his name at least every 2.5 episodes
WEIN - The hopf fibration is the only non-trivial principal bundle that can be visually seen
WEIN - since the world seems to be about principal bundles, it’s a bit odd that the general public doesn’t know that stuff of which we are.
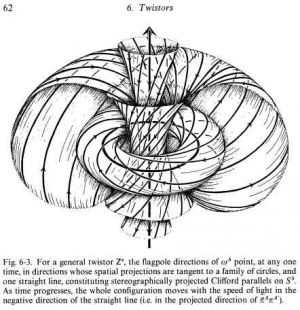
PEN - The “Hopf fibration”, or the “Clifford Parallels” was instrumental in the subject of Twistor Theory.
14:00 = Penrose’s diagram
There were three versions. The third version is in The Road to Reality. He thinks the second version is probably the best.
(I think they are talking about the diagram of the Hopf Fibration ?? as seen at the link above )
I think this is the one from “The Road to Reality”, which would make it Version 3: * **
please correct this if you know betterimage alt text
There’s also this diagram, which I found at a blog here: http://arkadiusz-jadczyk.eu/blog/tag/penrose/
And there’s this diagram, which I found at this link ( http://users.ox.ac.uk/~tweb/00001/ ) which is an HTML presentation of “On the Origins of Twistor Theory” - Roger Penrose, 1987
[NOTE: these latter two might be Versions 1 and 2? Or later reproductions.]
Penrose thinks Version 2 was the best.
WEIN - Dirac famously brought in these bizarre objects called Spinors, which are a prerequisite to getting to Twistors.
Dirac’s Spinors
Paul Dirac
15:00 = Dirac gave a course (2 courses) of lectures on Quantum Mechanics
Course 1 - Basic Quantum Mechanics
Course 2 - Quantum Field Theory but also Spinors
In the second course (when Penrose took the course) Dirac deviated from his normal course of lectures to give two or three lectures on Two Component Spinors. (Spinors)
WEIN - For the lay audience… If we think of all of matter as waves, the question is "what medium are they waves in? And the medium would be a medium of Spinors, which is not something that’s easy for people to understand.
Denis recommended to Roger a book by Corson (presumably this one: Introduction to Tensors, Spinors, and Relativistic Wave-Equations, 1953 by E.M. Corson *
The book was reviewed by Abdus Salam in 1955 (https://www.nature.com/articles/175831b0 )
<<<Dr Corson doesn’t seem to have a Wikipedia page which is a shame, considering some of the people who do
Roger found the book incomprehensible.
But then he took Dirac’s (2nd) course.
Dirac talked about Two Component Spinors and this was exactly what Roger needed.
Other people said that Dirac’s course was just like his book but Roger hadn’t read the book.
(I assume this one? Dirac - Principles of Quantum Mechanics)
18:00 = WEIN - "do you think Dirac understood (Spinors)?…
Mention of Mathematicians:
- Wilhelm Killing
- “Lee”? - this Lee https://en.wikipedia.org/wiki/John_M._Lee was in Differential Geometry but was born in 1950. Maybe his father?
- Élie Cartan
WEIN - let me throw out a dangerous idea. I don’t think any of us understand them (Spinors) .
WEIN - Dirac understood what could be said about Spinors
20:00 = PEN - "usually one talks about the Dirac Spinors, which are the 4 spinors, but they split into these 2 and 2 (WEIN - in even dimensions) Yes, that’s right.
Sir Roger Penrose’s favourite film is 2001: A Space Odyssey
Geometric Interpretation of Spinors
Roger describes the way he thinks of spinors geometrically.
“I had this picture of a flag. You have the flag-pole, goes along the light-cone (WEIN - that’s the vector-like piece of it) and then you have an extra piece of data which is this flag plane. You get a pretty good geometrical understanding. The one little catch is that if you rotate it through 360 degrees, so you might think just to where it started, it’s not the same as before, it’s changed its sign.”
Taken from Introduction to Spinors - Andrew M Steane 2013 (pdf)
WEIN: Klein Bottle:
Interlude: Klein Bottles
Get your Klein Bottle today from our friends at Acme Klein Bottles
Here’s a good video about Klein Bottles
(the presenter is Clifford Stoll, Astronomer and proprietor of Acme Klein Bottles )
- The Klein Bottle is “two Möbius Strips stitched together” (after August Ferdinand Möbius)
- The Klein Bottle is named after Felix Klein
- The Klein Bottle only has one side
- Klein bottles is 3D Universes must have a self-intersection
- Klein hats are continuously deformable back to themselves
- Clifford’s friend, Robert Lang, made an Origami Klein Bottle *
Here is another, related video, also from Numberphile, about the Topology of a Twisted Torus
<<<NB: This is a link to the actual pattern so that you can make your very own Origami Klein bottle.
This video is about slicing up toroids. The presenter is Carlo H. Séquin. Later in the podcast, Roger talks about the Clifford Parallels dividing up space in a similar way. This helped me to visualise that.
<<<One of his sculptures is not far from where I live. May have to make a visit.
It also introduced me to Keizo Ushio who makes amazing toroidal sculptures, like this one *
(source)
Here is an interview with Keizo Ushio.
In this video he can be heard speaking in English.
And here is a limerick about Klein bottles.
A mathematician named Klein
Thought the Moebius band was divine
Said he: "If you glue
The edges of two
You’ll get a weird bottle like mine."
(source) *
There are some more interesting (if somewhat amateur) visualisations in this Youtube video, from which I learned:
- The Klein Bottle is a non-orientable, 2-dimensional manifold.
- It can be “immersed” into Euclidean 3-dimensional space with a self-intersection.
- Non-orientable means “there exists no continuous normal unit vector field”
<<<Also relevant:
A mathematician confided
That the Moebius band is one-sided
And you’ll get quite a laugh
If you cut one in half
’Cause it stays in one piece when divided.
The Square Root of the Klein Bottle (Weyl’s Cones)
21:00 = WEIN - The Klein bottle has (in certain sense that can be made precise) a square-root that is a torus.
[Note: googling for “the square root of the Klein Bottle” didn’t get me far but searching for “double cover” I got useful things like this question on math Stackexchange, where someone has drawn this:
And the top respondent says “Most topologists would be happy just drawing the diagram you’ve drawn” (to prove that there is a two-sheeted covering of the Klein bottle by the Torus)
Reading that answer and then this one: https://math.stackexchange.com/questions/140439/torus-as-double-cover-of-the-klein-bottle gave me a pretty good idea of what’s going on.]
WEIN - It’s really the square-root of the rotations that has this double effect (but we say it linguistically in a way that makes it impossible for anyone to understand)
PEN - I understood that a spinor was the square root of a vector and I couldn’t make head of tail of it. When I went to Dirac’s course it did make sense.
Dirac gave a demonstration due to Hermann Weyl of rolling one cone on another
Here is a google-books link to Penrose describing the same model in the Hermann Weyl Centenary Lectures.
This site also has a description of the model (http://www.weylmann.com/2010archive.shtml - you need to search for the word “cone” to find the right article) and lots of other information about Weyl himself. It includes this diagram to illustrate the model:
The author of the site is William O. Straub and he has written other papers about Spinors, including eg; Weyl Spinors and Dirac’s Electron Equation.
This video on Youtube is a visualisation of rolling one coin around another.
22:00 =
PEN - You imagine increasing the semi-angle of the cone until it becomes almost flat. And then what’s the other one? It’s just a little wobble.
This demonstrates
WEIN - with a pulley system
In the place where you can see this most easily, it’s slightly confusing.
23:50 = WEIN - “we have to use the visual cortex we’re handed and then we have to trick it into imagining worlds beyond where we’ve seen.”
Ad Break
24:00 = advert for supplements.
25:00 = advert for online courses
26:00 =
Dirac’s Scissors
Dirac’s scissors, aka the Plate Trick, (related to?) the Belt Trick
Air on a Dirac String: https://www.youtube.com/watch?v=CYBqIRM8GiY
Fermions have a spin which is half an odd number. They have this curious property that rotate them and they get back to minus themselves. And it’s crucial for matter.
Without this, we wouldn’t have anything.
Bosons are the opposite. They’d rather like to be in the same state. For the Fermions it’s completely the opposite.
The Spin Statistics Theorem - "if things have a spin of a
When we want to treat these objects quantum mechanically, we have two
PEN - well, you’ve got these two types of matter.
34:00 = Phlogiston
[NOTE: Phlogiston was the supposed substance that inhered in bodies capable of combustion
Apropos of nothing much, I have always loved this quote about writing:
“The real writer is one who really writes. Talent is an invention like phlogiston after the fact of fire. Work is its own cure. You have to like it better than being loved.”
]
Maxwell’s Equations
35: 00 = “Maxwell’s Equations completely changed our way of looking at the world”
Faraday had a lot of the influential ideas.
Faraday had clues that there were connections to light, but he didn’t have the equations.
Charles Darwin
Book: Darwin - ON THE VARIOUS CONTRIVANCES BY WHICH BRITISH AND FOREIGN ORCHIDS ARE FERTILISED BY INSECTS, AND ON THE GOOD EFFECTS OF INTERCROSSING. BY CHARLES DARWIN, M.A., F.R.S., &c. WITH ILLUSTRATIONS.
In which Eric claims Darwin reveals that he did not understand his own theories.
Aharonov, Escher, Bohm
This bizarre effect of passing an electron around an insulated wire
The gentleman mentioned is Yakir Aharonov *
They are talking about the Aharonov–Bohm effect *
<<<or possibly the related Al’tshuler-Aronov-Spivak effect? Where ‘Aranov’ is a different person? I’m pretty sure it’s the aharanov-Bohm effect
We learned that if you have an insulated solenoid, the phase of the electron beam going in a circle around it would be shifted despite the fact that the electromagnetic field could be treated as zero because the electromagnetic potential, this precursor, had been shown to carry the actual content… it turned out that geometric object was more important
38:00 = MC ESCHER - Ascending and Descending (The Penrose Stairs)
Ascending and Descending - M.C. Escher
39:00 = PEN - anecdote about visiting Amsterdam. Mentions Shaun Wyile *
this is a guess, please check I have the right person
41:00 = “I played around with this and whittled it down to the triangle which people refer to as a ‘tribar’.” NB: He’s being modest and we actually call it a Penrose Triangle. (Penrose Triangle on Wolfram)
I’m pretty sure this is the paper: impossible objects a special type of visual illusion - L.S. Penrose and R. Penrose *
<<<NB: Wiley want $7 to rent this 62 year old paper for 48 hours (!) or $42 (!!) to buy it as a PDF. It is on SciHub and is 3 pages long. If you had to buy Penrose’s (paperback) book (tRtR) for the same per-page price, it would cost $14,000 a copy
Escher gave Penrose a print and it is in the Ashmolean Museum
<<<I can’t read this article: https://www.thetimes.co.uk/article/roger-penrose-on-his-friend-mc-escher-the-genius-that-galleries-ignored-90nhp8gsd0l because it’s behind a paywall, but the google link-summary says “… and he chose Fish and Scales, now on loan to the Ashmolean in Oxford”
(I think) the print was Fishes and Scales *
43:00 =
Eric Explains General Relativity
You have to begin with 4 degrees of freedom
Then you put rulers and protractors into it
That rise is
Those don’t fit together
The degree of “Escher-ness”
You throw one of them away, called the Weyl
That’s a long causal chain, but it is an accurate
Cohomology
It also illustrates co-homology.
What can you use Twistor-theory for? You can use it to solve Maxwell’s equations.
the movie inception
But that effect is the soul of the Aharanov-Bohm effect
We’ve mistold our stories
You were quite close to Michael Atiyah
His partner was Isadore Singer
They came up with the Atiyah-Singer Index Theorem which governs worlds in which there are no time dimensions but only space dimensions, or only time dimensions but no space
PEN - they could be just equations
Soap films look like elliptic equations
PEN - Atiyah-Singer is extremely general
WEIN - it tells you that… some high dimension… topological knotedness tells you something about the kinds of waves that can dance on that space.
53:00 =
Is The Real World Complex?
How to make Twistor-theory work in curved spaces
I ran into a problem that had to do with complex geometry.
Complex Geometry:
The analysis is particularly fascinating.
When you talk about real numbers, you can draw a function.
Smooth? Continuous? Curvature? How many degrees of smoothness? 1,2,3,4 or infinite?
Then we learn about complex. Do it all again using complex numbers and suddenly you find that if it’s smooth, everything comes with it.
WEIN - mathematicians quite often view the case of complex numbers as the natural case.
WEIN - You (Penrose) have been instrumental in making the case
…and then I learned about Quantum Mechanics. Yeah - there they are!
Suddenly these numbers are right there at the base of the subject
Minkowskian Geometry
57:00 = One of the ways of explaining what Twistor theory is
You are taking space-time and replacing it
You can ‘pull it upstairs’ to this Twistor space
Has this complex-number baked into it.
PEN - these things come together and take many years, sometimes, before they come together.
I was struck by the fact that
According to Einstein, special relativity, objects get flattened
It was these two-component spinors
If you think about the sky
Think of vector which is something that has a magnitude and also a direction to it.
You have particular vectors that you call ‘null’ - these are the ones along the light cone.
1:00 = in Minkowskian Geometry
1:01 = Minkowski showed
One event, say, and the light from that event reaches… a position in space time.
An event, or a point, in space-time
Imagine a particle moving between two points.
Minkowski realised that special-relativity is best described by this Minkowskian geometry.
Your idea was…
PEN - it took years but the initial idea isn’t so hard to understand.
If you look up in the sky, what are you seeing?
The world-line of that photon is ‘tilted over’
Suppose the photon is emitted at one event and received at another event.
That time measure is
Suppose you travel to a planet that is 8 light years away
Less than the time that someone on Earth would think it took you to get there.
And if you actually travel the speed of light, that time would be zero.
You’re not travelling at the speed of light, because you can’t get to the speed of light.
Even people who do this day and night choose never to work in some world.
If you go back and look at when Einstein introduced his relativity.
In that innocent decision to break off one degree of freedom and treat it different.
The Twistor Theory Cult
1:06 = “at that time, mathematicians and physicists were barely talking to each other”
Roman Jackiw - “when we talked to the geometers, we started to learn new things”
Jakiw is interviewed here at aip *
Schwarzchild Singularity - what we’d now call a ‘horizon’
<<<I haven’t found the direct quote, if you can find it, add a link
1:10 = you were sort of seen as running a cult
1:11 = PEN - “let me describe the basics of (Twistor Theory)”
Twistor Theory
Let me think of it the other way round, that is my past light cone
Imagine this cone stretching out into the past
Those stars in the sky look like points.
WEIN - imagine the world is transparent?
PEN - no, let’s go out into space
An astronaut whizzing by looks up.
Thanks to aberration, these will not be in quite the same place
It’s distorted, but it’s distorted conformally
If I see a circle, the astronaut will also see a circle
The thing about that transformation - something I knew about
You think about the Riemann Sphere
The Reimann Sphere and a Candy (or Toffee) Apple
The Riemann sphere folds all this up.
If you had a caramel coating around an apple (a Candy Apple) and at the point where the stick goes into that apple.
And it (the Riemann Sphere) has this property that it’s conformal.
The transformation is ‘analytic’ or ‘holomorphic’
WEIN - the analog of smooth for real numbers
Those transformations which send the sphere to the sphere are exactly those in Relativity.
The mapping from their sky to my sky is exactly this
And you get these two-component spinors
People find this puzzling. I find it puzzling!
The boundary of the thing will remain a circle.
Low-dimensional coincidences
Spinors grow exponentially whereas vectors grow linearly.
The rotations of space and time
When you do it (relativity) in the two spinor form.
Complex one-dimensional space.
Each complex number carries the information of two real numbers
The complex line
The language is intended to make things hostile to the newbie *
<<<Is it really intended for that purpose? Is it “the DISC”?
An object with the smallest spin you can have. Spin 1/2
(I think this is what’s called the Right-hand Screw Rule)
The complex numbers come in to describe these possible directions of spin.
These rather abstract numbers and the concrete directions in space.
The World is Given Only Once
1:22 = WEIN - “do you wed yourself to the world that’s given”
“the world is given only once”, attributed to Ernst Mach
“Do you wish to have a more general theory?”
What I see you having done is to work with mathematics that are particularising themselves to the world we live in.
1:23 = “You’re getting married to the world while other people are dating it, trying to keep their options open”
String Theory: People talk about (high) dimensions and, sure, we’ve got mathematics to describe that.
PEN - I’m looking for a way to describe the world that’s very particualar to the world we see
10 is two more than 8 and in 8 you have triality.
WEIN - “They (string theorists) never grow up to playing with reality”
PEN - I’m looking for a route that works specifically for the dimensionality we have
WEIN - If there weren’t a beautiful mathematics to catch you. You’re stage diving at a punk concert…
… the political economy of science means fewer people are willing to make strong predictions.
A dying breed of people who are prepared to go down with the ship for the privelege of commanding it.
Yours has been one of the most important, idiosyncratic programmes.
It is at least a deep insight into how to transform one problem into another to allow solutionis that wouldn’t have been easily gleaned in the original formulation.
WEIN - “do you believe Twistors are a more fundamental description of the world?”
PEN - “I do, yes. I don’t usually say that out loud”
WEIN - “I think that’s fucking great”
1:27 = one of the aims of mathematics is being more and more general
Deformation Complexes: 1st term - symmetries, 2nd - fields/waves, 3rd - equations
Cut it off at that point and have an elliptic complex
In dimension 4 we glean, something bizarre, that there are infinite ways to do calculus in 4 dimensional space and only one way to do it in every other dimension.
WEIN - Maybe differentiable structures are part of Physics
PEN - it’s quite possible
A Brief Critique of Particle Physics
If you have two Lie groups that act transitively on the same sphere in usual position, then either their intersection acts transitively on that sphere or the dimension of that sphere is 15. And I believe the intersection of the groups looks like the electro-strong group.
PEN - “I’ve never been someone who studied particle physics closely”
Pulled out of nowhere just by talking about sphere-transitive group actions.
Particle Physics?
We may be a long way from understanding what’s going on there.
WEIN - I didn’t know that
WEIN - I think we’re almost at the end
PEN - Understanding why the groups are the groups that we see.
1:30 = let me ask you a couple of questions
People like:
Unifying symmetries that remain very odd because they’re so attractive and powerful.
<<<This guy seems to have a very wide variety of interests. I double checked I have the right person and it seems right but please change it if you know differently.
The prettiest of them being spin-10, which physicists insist on calling SO 10 for reasons that escape me.
PEN - “Is this the one that doesn’t exist?”
Spin-5 (lives inside spin-10) was disproven
WEIN - Glashow and Georgi “rushed to commit ritual suicide far too quickly”
PEN - from the outside, I’m not convinced that…
Somehow (particle physics) has not got to the point… I’m hoping that Twistor theory might have something to say about it but the area that needs to be explored hasn’t been explored"
Particles in Twistor Theory
PEN - there was a question about how we treat massive particles in Twistor theory.
Twistor theory describes massless things.
Massless things have a privileged treatment.
PEN - There is a way of describing the Maxwell equations …which comes directly out of Twistor theory.
If you want to talk about massive particles, the way it seems to lead you is
A massive particle has a momentum vector which is time-like, so it points within the cone.
One way you can describe a time-like one is to think of two null ones. So you think of a zig-zag, so it’s got a zig and a zag and that’s one convenient way of doing it.
Or you might have one that’s made of three: zig, zag, zog - something like that.
You can get at the time-like line, it can be built from primitives.
You get these groups in Twistor theory and they look like the particle physics groups.
You get SU-2 and SU-3
SU-2 is ubiquitous and does not impress Eric.
but SU-3, representing the strong force, can be gauged to give QCD (genuine gauge theory)
Weak isospin.
Gauging doesn’t really work for SU-2
It’s not the full group and so on and there’s something wrong with it
1:34 - this is all guessing
The idea is you could develop a particle physics using many Twistors.
We have a problem in the standard model. We have an origin story with two gods.
The God of Einstein and the other god of SU-2 x SU-3.
The other gives us the quantum numbers.
This has no connection to the space and time data.
PEN - “they must be tied up at some stage but we haven’t got to that”
The idea was to do it via twistors.
When people discovered Charm this suddenly didn’t fit.
By charm you mean the addition of entirely separate versions of the familiar family of matter.
The addition of genera
1:36 = PEN - “I think we should go back to that”
Twistor Theory starts off as a theory about flat space-time
WEIN - “that’s what bothers me”
Origins of Twistor Theory
1:37 = PEN - “… the question is where did twistor theory come from”
WEIN - The Riemann Sphere of a with the Riemann Sphere of b
The world we see is Real numbers but the dynamics is controlled by the complex numbers.
Space-time has 4 dimensions.
Wanted to add another one because I wanted to incorporate an idea that was
Think of a Riemann sphere again
Complex numbers on one side and again on the other.
Rather than splitting everything into fourier components
Space-time is 4 dimensional and if you try to complexify it, you get 8 dimensions
1:39 = PEN - Anecdote about the day the JFK was shot and the day after when they visited San Antonio.
He travelled back with István Ozsváth * who didn’t speak much and started to think about
these constructions of Ivor Robinson * (in Dallas) which were solutions to the Maxwell equations that had these curious twists in them. I’d understood these things and realised that they were described by the Hopf map or the Clifford Parallels:
<<<I think? This was another hard one to look for.
<<<Please correct any links that you think are wrong?
Hopf fibration/Clifford parallels: https://en.wikipedia.org/wiki/Hopf_fibration
Robinson Congruences
You can think of a three dimensional sphere in four dimensions and you have these circles which fill the whole space, no two intersect and every two link. Beautiful configuration. This was the thing that geometrically described the solutions Ivor had found.
Think of a light ray and then think of all the light rays that meet that one and that family of light rays, you could have solutions of Maxwell’s equations that point along those rays.
It pushes the light ray into the complex.
You don’t see the light ray anymore.
You describe it by this family.
As I called them later, Robinson Congruences.
Six-dimensional family.
And one dimension, they can twist one way or the other.
WEIN - and that had three complex dimensions
PEN - it was a complex-projected three-space.
You have a 5-dimensional space that divides this 6-dimensional space into two.
1:44 - Isadore Singer took the work of Jim Simons and Frank Yang and on the trip to Oxford said “oh my god, this is the quaternionic rather than the complex hopf fibration”. He realised the self-dual equations were going to be a revolution.
1:45 = 4 complex dimensions means 8 real dimensions.
The Wu Yang Dictionary
WEIN - I am not a devotee of String Theory, nor of Loop Quantum Gravity
1:47 = if you look at curvature.
The Wu Yang dictionary. A geometer who becomes the most successful hedge fund manager in human history (Wu) meets a physicsist (Yang) *
<<<I’m confused about who the hedge fund manager is ? When I look up the two scientists I can’t see any mention of a hedge fund. Have I mis-identified one of them?
Steenrod’s fibre bundles (Norman Steenrod)
Charles Ehresmann, Ehresmannconnections, vector potentials and what have you
Geometric quantisation revolution
Heisenberg’s uncertainty relations come out of curvature
The pre-quantum line bundle
The key point is that what we’d previously treated as the annoyance of the HUP now became the beauty… the underlying quantum theory is now geometric.
Michael Atiyah
This weird grab bag that is called QFT - regimes where the number of particles changes, you need QFT, you can’t do it in QM.
QFT would have been discovered by topologists and geometers.
These are three separate revolutions. With people noones ever heard of. *
This thing, which is as gorgeous as anyting I’ve ever seen
What the F? Am I wildly off?
Quillam Theory?
1:51 = if you find the way through this you will really find the key.
That’s picked up a beautiful area of mathematics and turned it into physics.
I think there are things that are hiding in there.
What do you make of the fact that we now have three separate geometries?
- Reimannian Geometry - Parent of General Relativity
- Ehresmannian Geometry - Parent of the Maxwell Theory, also strong/weak force
- And then you’ve got this other geometric theory which is the geometric quantum.
Simons and Yang find … has gauge theory
Because Einstein takes curvature and uses something called
The opportunity to use gauge theory is lost.
He did this amazing thing by developing relativity.
He died before Quarks
There are huge, beautiful things in Mathematics and they do have a role.
The way the world works depends on deep mathematics.
They can be generalising ideas and revealing all sorts
The proportion of these that has relevance to Physics is very small
I’m sure that we will find other things, but the temptation is that there are so many directions
Once we had people who had a lot of different ideas.
Almost every new idea is dead on arrival unless you specifically keep it from predicting things that we don’t see.
A Brief Critique of String Theory
A class of “naughty boys” who get to make all sorts of claims…*
1:57 = “twistor theory is, at a minimum, an incredible valuable tool”
However, it’s also somewhat tolerated within the system
It’s a minority point of view but it’s allowed to play a parallel game to the String community.
String Theory is the smartest community out there - smarter than the relativists, smarter than the geometers, very clever and very insufferable.
The problem with that community is that they’ve accomplished a great deal that isn’t of a stringy nature.
Instead of quantising geometry, it backfired and they had the geometry geometrise the quantum. That’s the main legacy of these people.
They took off for Paris and landed in Tokyo. Very impressive as a feat but not what they intended to do.
I think I agree with that.
The influence I
Supersymmetry
What do you think about the legacy of something like Supersymmetry?
When I (Penrose) first heard of it
You needed complex analysis.
I visited (Bruno) Zumino
Deep supersymmetric model (the [model])
2:00 = Dirac had written this paper using two spinors - all the different spins with 2 spinors, clearer, etc.
Realised you could write it in
2:02 = Feynamn said these two things are proportional
Bell-Robinson Tensor
Bianci Identities written in 2-spinors
The higher the spin, the more indices
The Torsion Tensor
“We don’t really understand the things that we are given for free”
Re-deduces the Bianci identities
“I worry that we never really grounded these fields”
The torsion tensor.
Never shows up in any meaningful way anywhere.
2:04 PEN: I don’t use it.
what we have learned is of a very frightening nature.
Einsteins equations come from the simplest possible thing that could be optimised.
Dirac and the Bianci Identities
Dirac’s third equation is the equation for matter which generates all of something called K-theory, which is absolutely fundamental.
2:06 PEN: I wanted to finish a story
At one point Dirac was a fellow at the same college.
I said to him “would he have opportunity to talk to me about it”
I wrote down this wave equation that represents the Bianci equations
He asked where it came from and he said “what are the Bianci identities”
He simply re-discovered them himself, he didn’t know they were called the Bianci identities.
In vacuum, say, and you take the Weil curvature which is all that’s left of the Riemann curvature and you write that in spinors and it’s a spinor with four indices completely symmetrical and then when you write the derivative, it’s the derivative acting on those four things and one contraction - the derivative two indices and you contract one of those - and that’s your equation. That vanishes, that’s the equation. Same as the Maxwell equations, same as the neutrino if you have one index and no mass, and it’s the way I think about these things.
Did you read his 1963 article in
Against naive application of the scientific method.
He says Schrodinger would not have been led into error if he had not been pressed into agreement with experiment.
Secretly he was talking about himself.
Dirac trying to give us a gift from mount Olympus
Give yourself more room to play, to imagine and to be wrong.
2:10 PEN - Dirac didn’t like to be wrong. He was very worried about saying things that were wrong and so would say nothing.
The Future of Analytic Geometry
WEIN - Let me ask you a hard question… …you’re going to be in your 90’s soon
There’s a failure to pass torches. Who would you be pointing to?
PEN - A Human Being? …I don’t think I’m going to take you up on that one… …it’s proably someone I don’t know.
WEIN - Do you worry that the Oxford School of geometric physics won’t continue?
PEN - I suppose I do a bit.
WEIN - the UK tolerates and encourages personal idiosyncrasies.
- Nigel Hitchin
- Mason - possibly Lionel Mason?
- Philip Candelas
You’re asking me a bigger thing than… yeah
Penrose Tiles
Have you been to the courtyard of the Simons Centre for Geometry and Physics
They have a wall there - the so called iconic wall
They’re in a place that can be visited with a key and I always think about, in a fantastic world, unlocking that wall and seeing if it’s a gateway to something else.
2:15 = We all worry that we won’t get to see the end
What if I don’t get to see the end? Does that animates you?
There’s a huge amount of chance involved in these things. It’s all a gamble. *
TO see a real end is too remote
<<<Imagine how he must have seen the fellow-minds of his generation die, decade by decade
The Googly Problem
On the other hand we didn’t really discuss twistor theory - it’s been stuck and now it’s got unstuck.
The main theory
Construct solutions of the Einstein equations or the Ricci-flat which were completely
as long as they were anti-self dual
Why do we want complex solutions anyway?
Once I thought that the complex solutions were wavefunctions
I called in the non-linear graviton, which got stuck with the googly problem.
A googly is a ball bowled in the game of Cricket.
The ball bounces and to make it spin left-handed requires a special action but when you throw a googly, you use the same action which spins the ball left to instead spin it right.
I struggled and struggled and came up with all sorts of wild ideas and I found one that worked but it required a Cosmological Constant.
I was talking to
“That’s not the point, there are so many things that work better if you put this Cosmological Constant in”
It enables you to have a construction that enables you to solve the problem.
You talk about this algebra
Instead of patching
A point made clear to me by Michael Atiyah
This enables you to find a general solution of the Einstein equations.
But this is Lorentzian and not positive definite.
And that’s not the thing I’m good at doing
WEIN - sounds like you need a collaborator?
WEIN - stay away from that consciousness stuff
WEIN - stick with what you’ve done in Physics and try ot push that ball forwards.
WEIN - people are hungry to hear what it sounds like
PEN - as important as the details if not more.
2:22 = Thank You Very Much
Please subscribe to us wherever you listen to podcasts and subscribe to us on youtube.
Transcript
Resources
Notes
There were three versions. The third version is in The Road to Reality. He thinks the second version is probably the best.
MC ESCHER - Ascending and Descending (The Penrose Stairs)
Experimental Markup for player
physics
bizarreness he was difficult to get to
in my estimation if not yours Dirac
would be neck-and-neck with Einstein for
his hair I don't know well he didn't
about all we quantum mechanics people
Joe Rogan's program is to push out
discussion of the hopf fibration because
it's an it's the only non-trivial
principal bundle that can be visual
parallels was instrumental in the
of it the first one was more I sort of
circles in it and I thought I draw
version but actually I had three
road to reality but I'm not sure it's
understand the obsession called spinners
getting to twister theory which you've
quantum mechanics and the first course
the second course was on quantum field
theory but also spinners and there's an
my work on algebraic geometry we changed