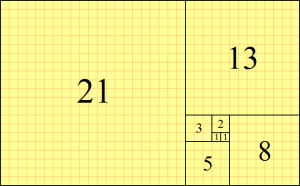
Fibonacci numbers
In mathematics, the Fibonacci numbers, commonly denoted [math]\displaystyle{ F_n }[/math], form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,
- [math]\displaystyle{ F_0=0,\quad F_1= 1, }[/math]
and
- [math]\displaystyle{ F_n=F_{n-1} + F_{n-2}, }[/math]
for [math]\displaystyle{ n \gt 1 }[/math].
The beginning of the sequence is thus:
- [math]\displaystyle{ 0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots }[/math]
The ratio [math]\displaystyle{ \frac {F_n}{F_{n+1}} \ }[/math] approaches the golden ratio as [math]\displaystyle{ n }[/math] approaches infinity.